10. Relations
Just as sets provide a convenient language for properties of the objects in a type, relations provide a convenient language for the properties of the pairs of objects in a type. This might sound dry and abstract, but such properties turn up all over mathematics: the property of one real number being less than another; the property of one integer being congruent to another modulo 5; the property of one set being a subset of another; the property of one function being inverse to another.
In this chapter we introduce some of the important properties which relations themselves can have: they can be reflexive, symmetric, antisymmetric or transitive, or any combination of these.
10.1. Reflexive, symmetric, antisymmetric, transitive
10.1.1. Example
Definition
A relation \(\sim\) on a type \(X\) is reflexive, if for all \(x\) of type \(X\), it is true that \(x\sim x\).
Problem
Prove that the relation \(|\) on \(\mathbb{N}\) is reflexive.
Solution
We must show that for all natural numbers \(x\), \(x\mid x\). Indeed, let \(x\) be a natural number; then \(x=x\cdot 1\).
example : Reflexive ((·:ℕ) ∣ ·) := by
dsimp [Reflexive]
intro x
use 1
ring
Definition
A relation \(\sim\) on a type \(X\) is symmetric, if for all \(x\) and \(y\) of type \(X\), if \(x\sim y\), then \(y\sim x\).
Problem
Prove that the relation \(|\) on \(\mathbb{N}\) is not symmetric.
Solution
We must show that there exist natural numbers \(x\) and \(y\) such that, \(x\mid y\) and \(y\mid x\). Indeed, we have \(2=1\cdot 2\), so \(1\mid 2\), and \(2\cdot 0<1<2\cdot 1\), so \(2\not \mid 1\).
example : ¬ Symmetric ((·:ℕ) ∣ ·) := by
dsimp [Symmetric]
push_neg
use 1, 2
constructor
· use 2
numbers
· apply Nat.not_dvd_of_exists_lt_and_lt
use 0
constructor
· numbers
· numbers
Definition
A relation \(\sim\) on a type \(X\) is antisymmetric, if for all \(x\) and \(y\) of type \(X\), if \(x\sim y\) and \(y\sim x\), then \(x=y\).
Problem
Prove that the relation \(|\) on \(\mathbb{N}\) is antisymmetric.
Solution
We first note the following fact (\(\star\)): if \(m\) and \(n\) are natural numbers with \(m=0\) and \(m\mid n\), then \(m=n\). Indeed, since \(m\mid n\) there exists a natural number \(k\) such that \(n=mk\), and then
We now return to the original problem. We must show that for all natural numbers \(x\) and \(y\), if \(x\mid y\) and \(y\mid x\), then \(x=y\). Indeed, let \(x\) and \(y\) be natural numbers and suppose \(x\mid y\) and \(y\mid x\). If \(x=0\) then by (\(\star\)) we are done; likewise if \(y=0\). Otherwise, \(x>0\), so since \(y\mid x\) we have \(y\le x\), and \(y>0\), so since \(x\mid y\) we have \(x\le y\), Putting these together, \(x=y\).
example : AntiSymmetric ((·:ℕ) ∣ ·) := by
have H : ∀ {m n}, m = 0 → m ∣ n → m = n
· intro m n h1 h2
obtain ⟨k, hk⟩ := h2
calc m = 0 := by rw [h1]
_ = 0 * k := by ring
_ = m * k := by rw [h1]
_ = n := by rw [hk]
dsimp [AntiSymmetric]
intro x y h1 h2
obtain hx | hx := Nat.eq_zero_or_pos x
· apply H hx h1
obtain hy | hy := Nat.eq_zero_or_pos y
· have : y = x := by apply H hy h2
rw [this]
apply le_antisymm
· apply Nat.le_of_dvd hy h1
· apply Nat.le_of_dvd hx h2
Definition
A relation \(\sim\) on a type \(X\) is transitive, if for all \(x\), \(y\) and \(z\) of type \(X\), if \(x\sim y\) and \(y\sim z\), then \(x\sim z\).
Problem
Prove that the relation \(|\) on \(\mathbb{N}\) is transitive.
Solution
We must show that for all natural numbers \(a\), \(b\) and \(c\), if \(a\mid b\) and \(b\mid c\) then \(a\mid c\).
Indeed, let \(a\), \(b\) and \(c\) be natural numbers with these properties. Since \(a\mid b\) there exists a natural number \(k\) such that \(b=ak\), and since \(b\mid c\) there exists a natural number \(l\) such that \(c=bl\). We then have
so \(a\mid c\).
example : Transitive ((·:ℕ) ∣ ·) := by
dsimp [Transitive]
intro a b c hab hbc
obtain ⟨k, hk⟩ := hab
obtain ⟨l, hl⟩ := hbc
use k * l
calc c = b * l := by rw [hl]
_ = (a * k) * l := by rw [hk]
_ = a * (k * l) := by ring
10.1.2. Example
Problem
Determine which of these properties hold for the relation \(=\) on \(\mathbb{R}\):
reflexive;
symmetric;
antisymmetric;
transitive.
example : Reflexive ((·:ℝ) = ·) := by
dsimp [Reflexive]
intro x
ring
example : Symmetric ((·:ℝ) = ·) := by
dsimp [Symmetric]
intro x y h
rw [h]
example : AntiSymmetric ((·:ℝ) = ·) := by
dsimp [AntiSymmetric]
intro x y h1 h2
rw [h1]
example : Transitive ((·:ℝ) = ·) := by
dsimp [Transitive]
intro x y z h1 h2
rw [h1, h2]
10.1.3. Example
Problem
Determine which of these properties hold for the relation \(\sim\) on \(\mathbb{R}\), defined by, \(x\sim y\) if \((x-y)^2\leq 1\):
reflexive;
symmetric;
antisymmetric;
transitive.
local infix:50 "∼" => fun (x y : ℝ) ↦ (x - y) ^ 2 ≤ 1
example : Reflexive (· ∼ ·) := by
dsimp [Reflexive]
intro x
calc (x - x) ^ 2 = 0 := by ring
_ ≤ 1 := by numbers
example : Symmetric (· ∼ ·) := by
dsimp [Symmetric]
intro x y h
calc (y - x) ^ 2 = (x - y) ^ 2 := by ring
_ ≤ 1 := by rel [h]
example : ¬ AntiSymmetric (· ∼ ·) := by
dsimp [AntiSymmetric]
push_neg
use 1, 1.1
constructor
· numbers
constructor
· numbers
· numbers
example : ¬ Transitive (· ∼ ·) := by
dsimp [Transitive]
push_neg
use 1, 1.9, 2.5
constructor
· numbers
constructor
· numbers
· numbers
10.1.4. Example
Consider the following finite inductive type Hand.
inductive Hand
| rock
| paper
| scissors
Consider the following relation \(\prec\) on the Hand type.
@[reducible] def r : Hand → Hand → Prop
| rock, rock => False
| rock, paper => True
| rock, scissors => False
| paper, rock => False
| paper, paper => False
| paper, scissors => True
| scissors, rock => True
| scissors, paper => False
| scissors, scissors => False
local infix:50 " ≺ " => r
Problem
Determine which of these properties hold for the relation \(\prec\):
reflexive;
symmetric;
antisymmetric;
transitive.
example : ¬ Reflexive (· ≺ ·) := by
dsimp [Reflexive]
push_neg
use rock
exhaust
example : ¬ Symmetric (· ≺ ·) := by
dsimp [Symmetric]
push_neg
use rock, paper
exhaust
example : AntiSymmetric (· ≺ ·) := by
dsimp [AntiSymmetric]
intro x y
cases x <;> cases y <;> exhaust
example : ¬ Transitive (· ≺ ·) := by
dsimp [Transitive]
push_neg
use rock, paper, scissors
exhaust
10.1.5. Exercises
Show that the relation \(<\) on \(\mathbb{R}\) is not symmetric.
example : ¬ Symmetric ((·:ℝ) < ·) := by sorry
Show that the relation \(\sim\) on \(\mathbb{Z}\), defined by, \(x\sim y\) if \(x\equiv y \mod 2\), is not antisymmetric.
local infix:50 "∼" => fun (x y : ℤ) ↦ x ≡ y [ZMOD 2] example : ¬ AntiSymmetric (· ∼ ·) := by sorry
Consider the following finite inductive type Little, and the following relation \(\sim\) on the Little type. Determine which of these properties hold for the relation \(\sim\):
reflexive;
symmetric;
antisymmetric;
transitive.
section inductive Little | meg | jo | beth | amy deriving DecidableEq open Little @[reducible] def s : Little → Little → Prop | meg, meg => True | meg, jo => True | meg, beth => True | meg, amy => True | jo, meg => True | jo, jo => True | jo, beth => True | jo, amy => False | beth, meg => True | beth, jo => True | beth, beth => False | beth, amy => True | amy, meg => True | amy, jo => False | amy, beth => True | amy, amy => True local infix:50 " ∼ " => s
example : Reflexive (· ∼ ·) := by sorry example : ¬ Reflexive (· ∼ ·) := by sorry example : Symmetric (· ∼ ·) := by sorry example : ¬ Symmetric (· ∼ ·) := by sorry example : AntiSymmetric (· ∼ ·) := by sorry example : ¬ AntiSymmetric (· ∼ ·) := by sorry example : Transitive (· ∼ ·) := by sorry example : ¬ Transitive (· ∼ ·) := by sorry
Determine which of these properties hold for the relation \(\sim\) on \(\mathbb{Z}\), defined by, \(x\sim y\) if \(y\equiv x+1\mod 5\):
reflexive;
symmetric;
antisymmetric;
transitive.
Also sketch (a representative portion of) this relation as a directed graph.
local infix:50 "∼" => fun (x y : ℤ) ↦ y ≡ x + 1 [ZMOD 5] example : Reflexive (· ∼ ·) := by sorry example : ¬ Reflexive (· ∼ ·) := by sorry example : Symmetric (· ∼ ·) := by sorry example : ¬ Symmetric (· ∼ ·) := by sorry example : AntiSymmetric (· ∼ ·) := by sorry example : ¬ AntiSymmetric (· ∼ ·) := by sorry example : Transitive (· ∼ ·) := by sorry example : ¬ Transitive (· ∼ ·) := by sorry
Determine which of these properties hold for the relation \(\sim\) on \(\mathbb{Z}\), defined by, \(x\sim y\) if \(x+y\equiv 0\mod 3\):
reflexive;
symmetric;
antisymmetric;
transitive.
Also sketch (a representative portion of) this relation as a directed graph.
local infix:50 "∼" => fun (x y : ℤ) ↦ x + y ≡ 0 [ZMOD 3] example : Reflexive (· ∼ ·) := by sorry example : ¬ Reflexive (· ∼ ·) := by sorry example : Symmetric (· ∼ ·) := by sorry example : ¬ Symmetric (· ∼ ·) := by sorry example : AntiSymmetric (· ∼ ·) := by sorry example : ¬ AntiSymmetric (· ∼ ·) := by sorry example : Transitive (· ∼ ·) := by sorry example : ¬ Transitive (· ∼ ·) := by sorry
Determine which of these properties hold for the relation \(\subseteq\) on \(\mathcal{P}(\mathbb{N})\), the type of sets of natural numbers.
reflexive;
symmetric;
antisymmetric;
transitive.
Also sketch (a representative portion of) this relation as a directed graph.
example : Reflexive ((· : Set ℕ) ⊆ ·) := by sorry example : ¬ Reflexive ((· : Set ℕ) ⊆ ·) := by sorry example : Symmetric ((· : Set ℕ) ⊆ ·) := by sorry example : ¬ Symmetric ((· : Set ℕ) ⊆ ·) := by sorry example : AntiSymmetric ((· : Set ℕ) ⊆ ·) := by sorry example : ¬ AntiSymmetric ((· : Set ℕ) ⊆ ·) := by sorry example : Transitive ((· : Set ℕ) ⊆ ·) := by sorry example : ¬ Transitive ((· : Set ℕ) ⊆ ·) := by sorry
Determine which of these properties hold for the relation \(\prec\) on \(\mathbb{R}^2\), defined by, \((x_1, y_1) \prec (x_2,y_2)\) if \(x_1\le x_2\) and \(y_1\le y_2\):
reflexive;
symmetric;
antisymmetric;
transitive.
local infix:50 "≺" => fun ((x1, y1) : ℝ × ℝ) (x2, y2) ↦ (x1 ≤ x2 ∧ y1 ≤ y2) example : Reflexive (· ≺ ·) := by sorry example : ¬ Reflexive (· ≺ ·) := by sorry example : Symmetric (· ≺ ·) := by sorry example : ¬ Symmetric (· ≺ ·) := by sorry example : AntiSymmetric (· ≺ ·) := by sorry example : ¬ AntiSymmetric (· ≺ ·) := by sorry example : Transitive (· ≺ ·) := by sorry example : ¬ Transitive (· ≺ ·) := by sorry
10.2. Equivalence relations
10.2.1. Example
Definition
A relation is an equivalence relation, if it is reflexive, symmetric and transitive.
Problem
Let \(n\) be an integer. Show that the relation \(\sim\) on \(\mathbb{Z}\) defined by, \(x\sim y\) if \(x\equiv y\mod n\) is an equivalence relation.
Solution
By Example 3.3.10, the relation \(\sim\) is reflexive.
By two of the exercises to Section 3.3, the relation \(\sim\) is symmetric and transitive.
variable (n : ℤ)
local infix:50 "∼" => fun (x y : ℤ) ↦ x ≡ y [ZMOD n]
example : Reflexive (· ∼ ·) := by
dsimp [Reflexive]
apply Int.ModEq.refl
example : Symmetric (· ∼ ·) := by
dsimp [Symmetric]
apply Int.ModEq.symm
example : Transitive (· ∼ ·) := by
dsimp [Transitive]
apply Int.ModEq.trans
Let’s sketch (a portion of) this relation as a directed graph, say for \(n=3\).

It’s a mess, but it’s just possible to make out a pattern: the numbers form cliques, with, for example, … -5, -2, 1, 4, 7, … all connected to each other and to nothing else. We introduce the following visual shorthand for such a directed graph: when nodes are given different colours, this represents the directed graph in which all nodes of a given colour are connected bi-directionally to all nodes of that colour (including themselves) and to no other nodes.
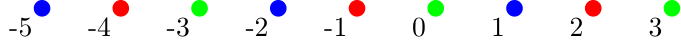
10.2.2. Example
Problem
Show that the relation \(\sim\) on \(\mathbb{Z}\) defined by \(a\sim b\) if \(a^2=b^2\) is an equivalence relation.
Solution
For all integers \(x\), we have \(x^2=x^2\), so \(x\sim x\). Therefore the relation \(\sim\) is reflexive.
For all integers \(x\) and \(y\), we have that if \(x\sim y\) then \(x^2=y^2\), so \(y^2=x^2\), so \(y\sim z\). Therefore the relation \(\sim\) is symmetric.
For all integers \(x\), \(y\) and \(z\), we have that if \(x\sim y\) and \(y\sim z\) then \(x^2=y^2\) and \(y^2=z^2\), so
so \(x\sim z\). Therefore the relation \(\sim\) is transitive.
local infix:50 "∼" => fun (x y : ℤ) ↦ x ^ 2 = y ^ 2
example : Reflexive (· ∼ ·) := by
dsimp [Reflexive]
intro x
ring
example : Symmetric (· ∼ ·) := by
dsimp [Symmetric]
intro x y hxy
rw [hxy]
example : Transitive (· ∼ ·) := by
dsimp [Transitive]
intro x y z hxy hyz
calc x ^ 2 = y ^ 2 := by rw [hxy]
_ = z ^ 2 := by rw [hyz]
If you try to sketch the directed graph for this relation, you will see that it has the same “clique” behaviour as the previous relation. After sketching the directed graph, sketch the multicoloured “clique” version.
10.2.3. Example
You have probably guessed that the colouring can be made consistent in this way for any equivalence relation. Let’s make this mathematically rigorous.
Let \(r\) be a relation on a type \(\alpha\), denoted \(\sim\) in infix notation.
Definition
For \(a\) in \(\alpha\), the equivalence class of \(a\) (denoted \([a]\)) is \(\{b:\alpha\mid a\sim b\}\).
Theorem
If the relation \(r\) is symmetric and transitive, then for all \(a_1\) and \(a_2\), if \(a_1\sim a_2\), then \([a_1]=[a_2]\).
Proof
We must show that for all \(b\) in \(\alpha\), \(a_1\sim b\) if and only if \(a_2\sim b\).
First, suppose that \(a_1\sim b\). Since \(a_1\sim a_2\), by symmetry \(a_2\sim a_1\), and so by transitivity \(a_2\sim a_1\sim b\).
Conversely, suppose that \(a_2\sim b\). Then since \(a_1\sim a_2\), by transitivity \(a_1\sim a_2\sim b\).
notation:arg "⦍" a "⦐" => { b | a ∼ b }
theorem EquivalenceClass.eq_of_rel (h_symm : @Symmetric α r) (h_trans : @Transitive α r)
{a1 a2 : α} (ha : a1 ∼ a2) :
⦍a1⦐ = ⦍a2⦐ := by
ext b
dsimp
constructor
· intro ha1b
apply h_trans (y := a1)
· apply h_symm ha
· apply ha1b
· intro ha2b
apply h_trans ha ha2b
Theorem
If the relation \(r\) is reflexive, then every \(a\) is an element of its own equivalence class: \(a\in [a]\).
Proof
We must show that for all \(a\), it is true that \(a\sim a\), and this is the definition of reflexivity.
theorem EquivalenceClass.mem_self (h_refl : @Reflexive α r) (a : α) :
a ∈ { b : α | a ∼ b } := by
dsimp
apply h_refl
10.2.4. Example
Consider the relation \(=\) on \(\mathbb{Z}\). It is an equivalence relation, by Example 10.1.2.
Exercise: Sketch this relation, by drawing (a portion of) the underlying type \(\mathbb{Z}\) along a line, then colouring each equivalence class in a different colour.
10.2.5. Example
Problem
Show that the relation \(\sim\) on \(\mathbb{Z}\times\mathbb{N}\) defined by, \((a,b)\sim(c,d)\) if \(a(d+1)=c(b+1)\), is an equivalence relation.
Solution
For all \((a,b)\) in \(\mathbb{Z}\times\mathbb{N}\), \(a(b+1)=a(b+1)\), so \((a,b)\sim (a,b)\). Therefore \(\sim\) is reflexive.
For all \((a,b)\) and \((c,d)\) in \(\mathbb{Z}\times\mathbb{N}\), if \((a,b)\sim (c,d)\) then \(a(d+1)=c(b+1)\), so \(c(b+1)=a(d+1)\), so \((c,d)\sim (a,b)\). Therefore \(\sim\) is symmetric.
For all \((a,b)\), \((c,d)\) and \((e,f)\) in \(\mathbb{Z}\times\mathbb{N}\), if \((a,b)\sim (c,d)\) and \((c,d)\sim (e,f)\) then \(a(d+1)=c(b+1)\) and \(c(f+1)=e(d+1)\). We will show that \(a(f+1)=e(b+1)\), which will imply that \((a,b)\sim (e,f)\), which proves the transitivity of \(\sim\).
Since \(d+1>0\), it suffices to prove that \((d+1)\left[a(f+1)\right]=(d+1)\left[e(b+1)\right]\). Let \(B:= b+1\), \(D:= d+1\), and \(F:= f+1\): then we know that \(aD=cB\) and \(cF=eD\) and need to prove that \(D(aF)=D(eB)\).
Indeed,
local infix:50 "∼" => fun ((a, b) : ℤ × ℕ) (c, d) ↦ a * (d + 1) = c * (b + 1)
example : Reflexive (· ∼ ·) := by
dsimp [Reflexive]
intro (a, b)
dsimp
example : Symmetric (· ∼ ·) := by
dsimp [Symmetric]
intro (a, b) (c, d) h
dsimp at *
rw [h]
example : Transitive (· ∼ ·) := by
dsimp [Transitive]
intro (a, b) (c, d) (e, f) h1 h2
dsimp at *
set B := (b:ℤ) + 1
set D := (d:ℤ) + 1
set F := (f:ℤ) + 1
have :=
calc D * (a * F) = (a * D) * F := by ring
_ = (c * B) * F := by rw [h1]
_ = (c * F) * B := by ring
_ = (e * D) * B := by rw [h2]
_ = D * (e * B) := by ring
cancel D at this
Now, sketch the relation \(\sim\), by drawing (a portion of) the underlying type \(\mathbb{Z}\times\mathbb{N}\) in the plane, then colouring each equivalence class in a different colour.
10.2.6. Example
Theorem
The relation \(\sim\) on the type of level-0 types defined by, \(\alpha\sim\beta\) if there exists a bijective function \(f:\alpha\to\beta\), is an equivalence relation.
local infix:50 "∼" => fun (α β : Type) ↦ ∃ f : α → β, Bijective f
example : Reflexive (· ∼ ·) := by
dsimp [Reflexive]
intro α
use id
rw [bijective_iff_exists_inverse]
use id
constructor
· rfl
· rfl
example : Symmetric (· ∼ ·) := by
dsimp [Symmetric]
intro α β h
obtain ⟨f, hf⟩ := h
rw [bijective_iff_exists_inverse] at hf
obtain ⟨g, hfg1, hfg2⟩ := hf
use g
rw [bijective_iff_exists_inverse]
use f
constructor
· apply hfg2
· apply hfg1
example : Transitive (· ∼ ·) := by
dsimp [Transitive]
intro α β γ h1 h2
obtain ⟨f1, hf1a, hf1b⟩ := h1
obtain ⟨f2, hf2a, hf2b⟩ := h2
use f2 ∘ f1
constructor
· apply Injective.comp
· apply hf2a
· apply hf1a
· apply Surjective.comp
· apply hf2b
· apply hf1b
10.2.7. Exercises
Consider the relation \(\sim\) on \(\mathbb{Z}\) defined by, \(a\sim b\) if there exist positive integers \(m\) and \(n\) such that \(am=bn\).
Show that \(\sim\) is an equivalence relation.
Sketch the relation \(\sim\), by drawing (a portion of) the underlying type \(\mathbb{Z}\) along a line, then colouring each equivalence class in a different colour.
local infix:50 "∼" => fun (a b : ℤ) ↦ ∃ m n, m > 0 ∧ n > 0 ∧ a * m = b * n example : Reflexive (· ∼ ·) := by sorry example : Symmetric (· ∼ ·) := by sorry example : Transitive (· ∼ ·) := by sorry
Consider the relation \(\sim\) on \(\mathbb{N}^2\) defined by, \((a,b)\sim(c,d)\) if \(a+d=b+c\).
Show that \(\sim\) is an equivalence relation.
Sketch the relation \(\sim\), by drawing (a portion of) the underlying type \(\mathbb{N}^2\) in the plane, then colouring each equivalence class in a different colour.
local infix:50 "∼" => fun ((a, b) : ℕ × ℕ) (c, d) ↦ a + d = b + c example : Reflexive (· ∼ ·) := by sorry example : Symmetric (· ∼ ·) := by sorry example : Transitive (· ∼ ·) := by sorry
Consider the relation \(\sim\) on \(\mathbb{Z}^2\) defined by, \((a,b)\sim(c,d)\) if there exist positive integers \(m\) and \(n\) with \(mb(b^2-3a^2)=nd(d^2-3c^2)\).
Show that \(\sim\) is an equivalence relation.
Sketch the relation \(\sim\), by drawing (a portion of) the underlying type \(\mathbb{Z}^2\) in the plane, then colouring each equivalence class in a different colour.
local infix:50 "∼" => fun ((a, b) : ℤ × ℤ) (c, d) ↦ ∃ m n, m > 0 ∧ n > 0 ∧ m * b * (b ^ 2 - 3 * a ^ 2) = n * d * (d ^ 2 - 3 * c ^ 2) example : Reflexive (· ∼ ·) := by sorry example : Symmetric (· ∼ ·) := by sorry example : Transitive (· ∼ ·) := by sorry