6. Induction
This chapter introduces induction, a proof method which applies to the natural numbers and to other discrete types such as integers or pairs of natural numbers. We also introduce recursion, a method for defining sequences (and, more generally, functions from discrete types); induction is the canonical method for proving results about recursively-defined objects.
In Section 6.1 - Section 6.3, we use only the most traditional form of induction, proving a result for a natural number by relating it to the result for the previous natural number, and small variants on this form of induction. In Section 6.4 - Section 6.7, we introduce strong induction, and, even more generally, well-founded induction. These induction principles are more flexible.
6.1. Introduction
6.1.1. Example
Problem
Let \(n\) be a natural number. Show that \(2 ^n\ge n+1\).
Solution
We prove this by induction on \(n\). The base case, \(2^0\geq 0+1\), is clear.
Suppose now that for some natural number \(k\), it is true that \(2 ^k\ge k+1\). Then
In Lean, the tactic simple_induction will set up an induction proof. Here, before the line
simple_induction n with k IH, the goal state displays a single goal,
n : ℕ
⊢ 2 ^ n ≥ n + 1
and after the tactic is used the goal state displays two goals, one for the base case and one for the inductive step.
⊢ 2 ^ 0 ≥ 0 + 1
k : ℕ
IH : 2 ^ k ≥ k + 1
⊢ 2 ^ (k + 1) ≥ k + 1 + 1
Here is the full proof in Lean.
example (n : ℕ) : 2 ^ n ≥ n + 1 := by
simple_induction n with k IH
· -- base case
numbers
· -- inductive step
calc 2 ^ (k + 1) = 2 * 2 ^ k := by ring
_ ≥ 2 * (k + 1) := by rel [IH]
_ = (k + 1 + 1) + k := by ring
_ ≥ k + 1 + 1 := by extra
6.1.2. Example
Theorem
Let \(n\) be a natural number. Then \(n\) is either even or odd.
(Compare Example 3.1.9, Example 4.2.9.)
Proof
We prove this by induction on \(n\).
The base case is to show that 0 is either even or odd. We will show that it is even. Indeed, \(0=2\cdot 0\).
Suppose now that for some natural number \(k\), it is true that \(k\) is either even or odd.
Case 1 (\(k\) is even): Then there exists an integer \(x\) such that \(k=2x\), and so \(k+1 = 2x+1\), so \(k+1\) is odd.
Case 2 (\(k\) is odd): Then there exists an integer \(x\) such that \(k=2x+1\), and
so \(k+1\) is even.
Here is the outline of this argument in Lean. Fill in the sorries.
example (n : ℕ) : Even n ∨ Odd n := by
simple_induction n with k IH
· -- base case
sorry
· -- inductive step
obtain ⟨x, hx⟩ | ⟨x, hx⟩ := IH
· sorry
· sorry
6.1.3. Example
Theorem
Let \(a, b, d\) be integers, and suppose that \(a\equiv b \mod d\). Let \(n\) be a natural number. Then \(a^n\equiv b ^ n \mod d\).
This is the power rule for modular arithmetic, the lemma Int.modEq.pow, which we stated without
proof in Example 3.3.9. It is one of the lemmas which are bundled together to
form the tactic rel’s capability for modular arithmetic.
Proof
We prove this by induction on \(n\).
We first note that \(a^0-b^0 = d\cdot 0\), so \(d\mid a^0-b^0\), so \(a^0\equiv b ^ 0 \mod d\). This is the base case.
Now, let \(k\) be a natural number, and suppose that \(a^k\equiv b ^ k \mod d\). Then there exists an integer \(x\) such that \(a^k- b ^ k =dx\). Also, by hypothesis, \(a\equiv b \mod d\), so there exists an integer \(y\) such that \(a-b=dy\). We then have
so \(d\mid a^{k+1}-b^{k+1}\), so \(a^{k+1}\equiv b ^ {k+1} \mod d\).
Write out this proof in Lean.
example {a b d : ℤ} (h : a ≡ b [ZMOD d]) (n : ℕ) : a ^ n ≡ b ^ n [ZMOD d] := by
sorry
6.1.4. Example
Problem
Let \(n\) be a natural number. Show that \(4^n\) is congruent to either \(1\) or \(4\) modulo 15.
Solution
We prove this by induction on \(n\). First, \(4^0=1\), so \(4^0\equiv 1\mod 15\).
Now, let \(k\) be a natural number, and suppose that we know that \(4^k\) is congruent to either \(1\) or \(4\) modulo 15.
Case 1 (\(4^k\equiv 1\mod 15\)): Then
Case 2 (\(4^k\equiv 4\mod 15\)): Then
example (n : ℕ) : 4 ^ n ≡ 1 [ZMOD 15] ∨ 4 ^ n ≡ 4 [ZMOD 15] := by
simple_induction n with k IH
· -- base case
left
numbers
· -- inductive step
obtain hk | hk := IH
· right
calc (4:ℤ) ^ (k + 1) = 4 * 4 ^ k := by ring
_ ≡ 4 * 1 [ZMOD 15] := by rel [hk]
_ = 4 := by numbers
· left
calc (4:ℤ) ^ (k + 1) = 4 * 4 ^ k := by ring
_ ≡ 4 * 4 [ZMOD 15] := by rel [hk]
_ = 15 * 1 + 1 := by numbers
_ ≡ 1 [ZMOD 15] := by extra
6.1.5. Example
We can also use induction to prove results about all natural numbers greater than a given number. We just start the induction at that number.
Problem
Let \(n\) be a natural number greater than or equal to 2. Show that \(3 ^n\ge 2^n+5\).
Solution
We prove this by induction on \(n\), starting at 2. The base case, \(3^2\geq 2^2+5\), is clear.
Suppose now that for some natural number \(k\), it is true that \(3 ^k\ge 2^k+5\). Then
In Lean, the tactic induction_from_starting_point will set up an induction proof starting at a
given point.
example {n : ℕ} (hn : 2 ≤ n) : (3:ℤ) ^ n ≥ 2 ^ n + 5 := by
induction_from_starting_point n, hn with k hk IH
· -- base case
numbers
· -- inductive step
calc (3:ℤ) ^ (k + 1) = 2 * 3 ^ k + 3 ^ k := by ring
_ ≥ 2 * (2 ^ k + 5) + 3 ^ k := by rel [IH]
_ = 2 ^ (k + 1) + 5 + (5 + 3 ^ k) := by ring
_ ≥ 2 ^ (k + 1) + 5 := by extra
6.1.6. Example
Induction from a nonzero starting point is a particularly useful technique for “sufficiently large” problems.
Problem
Show that for all sufficiently large natural numbers \(n\), \(2^n\geq n^2\).
Solution
We will show this for all natural numbers \(n\geq 4\).
We prove this by induction on \(n\), starting at 4. The base case, \(2^4\geq 4^2\), is clear.
Suppose now that for some natural number \(k\geq 4\), it is true that \(2 ^k\ge k^2\). Then
Here is the outline of this argument in Lean. Fill in the sorries.
example : forall_sufficiently_large n : ℕ, 2 ^ n ≥ n ^ 2 := by
dsimp
use 4
intro n hn
induction_from_starting_point n, hn with k hk IH
· -- base case
sorry
· -- inductive step
sorry
6.1.7. Exercises
Let \(n\) be a natural number. Show that \(3 ^n\ge n^2+n+1\).
example (n : ℕ) : 3 ^ n ≥ n ^ 2 + n + 1 := by sorry
Let \(a\geq -1\) be a real number, and let \(n\) be a natural number. Show that \((1+a)^n\ge 1+na\).
This fact is known as Bernoulli’s inequality.
example {a : ℝ} (ha : -1 ≤ a) (n : ℕ) : (1 + a) ^ n ≥ 1 + n * a := by sorry
Let \(n\) be a natural number. Show that \(5^n\) is congruent to either \(1\) or \(5\) modulo 8.
example (n : ℕ) : 5 ^ n ≡ 1 [ZMOD 8] ∨ 5 ^ n ≡ 5 [ZMOD 8] := by sorry
Let \(n\) be a natural number. Show that \(6^n\) is congruent to either \(1\) or \(6\) modulo 7.
example (n : ℕ) : 6 ^ n ≡ 1 [ZMOD 7] ∨ 6 ^ n ≡ 6 [ZMOD 7] := by sorry
Let \(n\) be a natural number. Show that \(4^n\) is congruent to \(1\), \(2\) or \(4\) modulo 7.
example (n : ℕ) : 4 ^ n ≡ 1 [ZMOD 7] ∨ 4 ^ n ≡ 2 [ZMOD 7] ∨ 4 ^ n ≡ 4 [ZMOD 7] := by sorry
Show that for all natural numbers \(n\) sufficiently large, \(3^n\geq 2^n+100\).
example : forall_sufficiently_large n : ℕ, (3:ℤ) ^ n ≥ 2 ^ n + 100 := by dsimp sorry
Show that for all natural numbers \(n\) sufficiently large, \(2^n\geq n^2+4\).
example : forall_sufficiently_large n : ℕ, 2 ^ n ≥ n ^ 2 + 4 := by dsimp sorry
Show that for all natural numbers \(n\) sufficiently large, \(2^n\geq n^3\).
example : forall_sufficiently_large n : ℕ, 2 ^ n ≥ n ^ 3 := by dsimp sorry
Let \(a\) be an odd natural number. Show by induction that for all natural numbers \(n\), the natural number \(a^n\) is odd.
Also deduce that for all natural numbers \(a\) and \(n\), if \(a^n\) is even then \(a\) is even. (This part is not an induction problem.)
theorem Odd.pow {a : ℕ} (ha : Odd a) (n : ℕ) : Odd (a ^ n) := by sorry theorem Nat.even_of_pow_even {a n : ℕ} (ha : Even (a ^ n)) : Even a := by sorry
6.2. Recurrence relations
6.2.1. Example
A sequence of numbers is an indexed list which goes on forever. Some sequences are defined by closed formulas. For example, \(a_n=2^n\) defines a sequence, the powers of two, with
In Lean, we would define this sequence as
def a (n : ℕ) : ℕ := 2 ^ n
and Lean will also calculate any term of the sequence we wish:
#eval a 20 -- infoview displays `1048576`
However, many important sequences do not have an easy closed formula. A more flexible way to define sequences is with a recursive definition. For example, we can define a sequence \((b_n)\) recursively by,
\[\begin{split}b_0&=3 \\ \text{for }n:\mathbb{N},\quad b_{n+1} &= b_n{}^2-2.\end{split}\]
The first few terms of this sequence are
In Lean, we would define this sequence as
def b : ℕ → ℤ
| 0 => 3
| n + 1 => b n ^ 2 - 2
and Lean will also calculate any term of the sequence we wish (up to the limits of its computational power!):
#eval b 7 -- infoview displays `316837008400094222150776738483768236006420971486980607`
When a sequence is defined recursively, it is convenient to reason about it by induction.
Problem
Show that for all \(n\), the integer \(b_n\) is odd.
Solution
We will prove this by induction on \(n\).
First, note that
so \(b_0\) is odd.
Now, let \(k\) be a natural number and suppose that \(b_k\) is odd. Then there exists an integer \(x\) such that \(b_k=2x+1\). We then have,
so \(b_{k+1}\) is also odd.
Here is that solution in Lean; note the use of rw [b] to unfold either piece of the recursive
definition of \(b\), as needed.
example (n : ℕ) : Odd (b n) := by
simple_induction n with k hk
· -- base case
use 1
calc b 0 = 3 := by rw [b]
_ = 2 * 1 + 1 := by numbers
· -- inductive step
obtain ⟨x, hx⟩ := hk
use 2 * x ^ 2 + 2 * x - 1
calc b (k + 1) = b k ^ 2 - 2 := by rw [b]
_ = (2 * x + 1) ^ 2 - 2 := by rw [hx]
_ = 2 * (2 * x ^ 2 + 2 * x - 1) + 1 := by ring
You might like to try giving another proof using the modular-arithmetic characterization of parity; this will work both in text and in Lean.
6.2.2. Example
Here is another recursively defined sequence:
\[\begin{split}x_0&=5 \\ \text{for }n:\mathbb{N},\quad x_{n+1} &= 2x_n-1.\end{split}\]
In Lean the definition looks like this:
def x : ℕ → ℤ
| 0 => 5
| n + 1 => 2 * x n - 1
Work out the first few terms of this sequence (or get Lean to do it for you!). Here is a property we can prove about the sequence \((x_n)\):
Problem
Show that for all natural numbers \(n\), \(x_n\equiv 1\mod 4\).
Solution
We prove this by induction on \(n\).
For the base case, observe that
For the inductive step, suppose that \(x_k\equiv 1\mod 4\) for some natural number \(k\). Then
also.
Write out the two parts of the proof of this statement in Lean.
example (n : ℕ) : x n ≡ 1 [ZMOD 4] := by
simple_induction n with k IH
· -- base case
sorry
· -- inductive step
sorry
6.2.3. Example
Sometimes, a sequence defined recursively can also be given a closed form expression. This is the case for the sequence \((x_n)\) from the previous problem.
Problem
Show that for all natural numbers \(n\), \(x_n=2^{n+2}+1\).
Solution
We prove this by induction on \(n\).
For the base case, note that as desired,
For the inductive step, suppose that \(x_k=2^{k+2}+1\) for some natural number \(k\). Then
example (n : ℕ) : x n = 2 ^ (n + 2) + 1 := by
simple_induction n with k IH
· -- base case
calc x 0 = 5 := by rw [x]
_ = 2 ^ (0 + 2) + 1 := by numbers
· -- inductive step
calc x (k + 1) = 2 * x k - 1 := by rw [x]
_ = 2 * (2 ^ (k + 2) + 1) - 1 := by rw [IH]
_ = 2 ^ ((k + 1) + 2) + 1 := by ring
6.2.4. Example
Here is one more recursively defined sequence:
\[\begin{split}A_0&=0 \\ \text{for }n:\mathbb{N},\quad A_{n+1} &= A_n + (n + 1).\end{split}\]
def A : ℕ → ℚ
| 0 => 0
| n + 1 => A n + (n + 1)
Let’s work out the first terms of this sequence:
\[\begin{split}A_0&=0 \\ A_1&=A_0+1 \\ &=1\\ A_2&=A_1+2 \\ &=1+2\\ &=3\\ A_3&=A_2+3 \\ &=3+3\\ &=6\\ A_4&=A_3+4 \\ &=6+4\\ &=10\\ \ldots\end{split}\]
Note the pattern: first we added 1, then 2, then 3, then 4. So in fact
\[\begin{split}A_1&=1 \\ A_2&=1+2 \\ A_3&=1+2+3 \\ A_4&=1+2+3+4\\ \ldots\end{split}\]
The term \(A_n\) of the sequence represents the sum of the numbers from 1 to \(n\).
Problem
Show that for all natural numbers \(n\),
Solution
We prove this by induction on \(n\). First note that
This establishes the base case. Now, let \(k\) be a natural number and suppose that \(A_k=\frac{k(k+1)}{2}\). We then have
Here it is in Lean, written with one fewer step because Lean is better at algebra than humans are.
example (n : ℕ) : A n = n * (n + 1) / 2 := by
simple_induction n with k IH
· -- base case
calc A 0 = 0 := by rw [A]
_ = 0 * (0 + 1) / 2 := by numbers
· -- inductive step
calc
A (k + 1) = A k + (k + 1) := by rw [A]
_ = k * (k + 1) / 2 + (k + 1) := by rw [IH]
_ = (k + 1) * (k + 1 + 1) / 2 := by ring
6.2.5. Example
We built the previous sequence by adding 1, then 2, then 3, etc. What if we do the same thing but for multiplication? This gives the so-called factorial function, with “\(n\) factorial” denoted \(n!\).
\[\begin{split}0!&=1 \\ \text{for }n:\mathbb{N},\quad(n+1)! &= (n + 1) ⬝ n!\end{split}\]
def factorial : ℕ → ℕ
| 0 => 1
| n + 1 => (n + 1) * factorial n
notation:10000 n "!" => factorial n
So
\[\begin{split}1!&=1 \\ 2!&=2\cdot 1 \\ 3!&=3\cdot 2\cdot 1 \\ 4!&=4\cdot 3\cdot 2\cdot 1.\\ \ldots\end{split}\]
Concretely,
\[\begin{split}0!&=1 \\ 1!&=1\cdot A_0 \\ &=1\cdot 1 \\ &=1\\ 2!&=2\cdot A_1 \\ &=2\cdot 1 \\ &=2\\ 3!&=3\cdot A_2 \\ &=3\cdot 2 \\ &=6\\ 4!&=4\cdot A_3 \\ &=4\cdot 6 \\ &=24\\ \ldots\end{split}\]
Problem
Let \(n\) be a natural number. Show that every natural number \(d\) with \(1\le d\le n\) is a factor of \(n!\).
Solution
We prove this by induction on \(n\). For the base case, \(n=0\), the statement is vacuous, since there is no natural number \(d\) with \(1\le d\le 0\).
Let \(k\) be a natural number and suppose that every natural number \(d\) with \(1\le d\le k\) is a factor of \(k!\). Now let \(d\) be a natural number with \(1\le d\le k+1\). We must show that \(d\) is a factor of \((k+1)!\).
Case 1 (\(d=k+1\)): We have that
so \(d\) is a factor of \((k+1)!\).
Case 1 (\(d<k+1\)): Then \(d\le k\), so by the inductive hypothesis \(d\) is a factor of \(k!\). Therefore there exists a natural number \(x\) such that \(k!=dx\). We then have
so \(d\) is a factor of \((k+1)!\).
Here is the same proof in Lean. We record it for future use under the name dvd_factorial.
example (n : ℕ) : ∀ d, 1 ≤ d → d ≤ n → d ∣ n ! := by
simple_induction n with k IH
· -- base case
intro k hk1 hk
interval_cases k
· -- inductive step
intro d hk1 hk
obtain hk | hk : d = k + 1 ∨ d < k + 1 := eq_or_lt_of_le hk
· -- case 1: `d = k + 1`
sorry
· -- case 2: `d < k + 1`
sorry
6.2.6. Example
Problem
Show that for all natural numbers \(n\), we have \((n+1)!\ge 2^n\).
Solution
We prove this by induction on \(n\).
For the base case,
For the inductive step, suppose that for some natural number \(k\), \((k+1)!\ge 2^k\). Then
example (n : ℕ) : (n + 1)! ≥ 2 ^ n := by
sorry
6.2.7. Exercises
Consider the sequence \((c_n)\) defined recursively by,
\[\begin{split}c_0&=7 \\ \text{for }n:\mathbb{N},\quad c_{n+1} &= 3c_n-10.\end{split}\]Show that for all natural numbers \(n\), the integer \(c_n\) is odd.
def c : ℕ → ℤ | 0 => 7 | n + 1 => 3 * c n - 10 example (n : ℕ) : Odd (c n) := by sorry
Let the sequence \((c_n)\) be defined as in the previous problem. Show that for all \(n\), \(c_n=2\cdot 3^n+5\).
example (n : ℕ) : c n = 2 * 3 ^ n + 5 := by sorry
Consider the sequence \((y_n)\) defined recursively by,
\[\begin{split}y_0&=2 \\ \text{for }n:\mathbb{N},\quad y_{n+1} &= y_n{}^2.\end{split}\]Show that for all natural numbers \(n\), \(y_n=2^{2^n}\).
def y : ℕ → ℕ | 0 => 2 | n + 1 => (y n) ^ 2 example (n : ℕ) : y n = 2 ^ (2 ^ n) := by sorry
Consider the sequence \((B_n)\) defined recursively by,
\[\begin{split}B_0&=0 \\ \text{for }n:\mathbb{N},\quad B_{n+1} &= B_n+(n+1)^2.\end{split}\]Thus \(B_n\) represents the sum \(1^2+2^2+3^2+\cdots+n^2\). Show that for all natural numbers \(n\),
\[B_n=\frac{n(n+1)(2n+1)}{6}.\]def B : ℕ → ℚ | 0 => 0 | n + 1 => B n + (n + 1 : ℚ) ^ 2 example (n : ℕ) : B n = n * (n + 1) * (2 * n + 1) / 6 := by sorry
Consider the sequence \((S_n)\) defined recursively by,
\[\begin{split}S_0&=1 \\ \text{for }n:\mathbb{N},\quad S_{n+1} &= S_n+\frac{1}{2^{n+1}}.\end{split}\]Thus \(S_n\) represents the sum \(1+\frac{1}{2}+\frac{1}{4}+\cdots+\frac{1}{2^n}\). Show that for all natural numbers \(n\),
\[S_n=2-\frac{1}{2^n}.\]def S : ℕ → ℚ | 0 => 1 | n + 1 => S n + 1 / 2 ^ (n + 1) example (n : ℕ) : S n = 2 - 1 / 2 ^ n := by sorry
Show that \(n!\) is strictly positive, for all natural numbers \(n\).
We record this for future use under the name
factorial_pos.example (n : ℕ) : 0 < n ! := by sorry
Show that \(n!\) is even for all \(n\geq 2\). Use induction from the starting point 2 (see Example 6.1.5).
example {n : ℕ} (hn : 2 ≤ n) : Nat.Even (n !) := by sorry
Show that for all natural numbers \(n\), \((n+1)!\le (n+1)^n\).
(Compare with Example 6.2.6.)
example (n : ℕ) : (n + 1) ! ≤ (n + 1) ^ n := by sorry
6.3. Two-step induction
6.3.1. Example
In the last section we studied recursively defined sequences in which each term is constructed from the previous term. But it is also possible to define a sequence recursively with reliance on several previous terms.
For example, here is a sequence defined recursively in terms of the two previous terms.
Notice that since the recurrence relation depends on two previous terms, we need to give two concrete values of the sequence (\(a_0=2\) and \(a_1=1\)) to start with.
The first few terms of this sequence are
In Lean, we would define this sequence as
def a : ℕ → ℤ
| 0 => 2
| 1 => 1
| n + 2 => a (n + 1) + 2 * a n
and, as in the previous section, Lean will calculate for us any term of the sequence:
#eval a 5 -- infoview displays `31`
Compute several more terms of the sequence, either on paper or with Lean’s help. You will start to see a pattern: every term of the sequence differs by one from a power of two. We can prove this pattern by induction.
Problem
Prove that for all natural numbers \(n\), \(a_n=2^n+(-1)^n\).
In the proof below, notice that there are two base cases and two inductive hypotheses. Think about why.
Solution
We prove this by induction on \(n\).
We have that
and
Now let \(k\) be a natural number and suppose that \(a_k=2^k+(-1)^k\) and \(a_{k+1}=2^{k+1}+(-1)^{k+1}\). Then
The first two steps (using the recurrence relation and the inductive hypotheses) of the main calculation are fairly fixed, but you might have more or fewer lines of endgame depending on your facility with exponent rules and mental arithmetic. Lean can do it all in one line!
We use the Lean tactic two_step_induction for this kind of induction with two base cases and two
inductive hypotheses.
example (n : ℕ) : a n = 2 ^ n + (-1) ^ n := by
two_step_induction n with k IH1 IH2
. calc a 0 = 2 := by rw [a]
_ = 2 ^ 0 + (-1) ^ 0 := by numbers
. calc a 1 = 1 := by rw [a]
_ = 2 ^ 1 + (-1) ^ 1 := by numbers
calc
a (k + 2)
= a (k + 1) + 2 * a k := by rw [a]
_ = (2 ^ (k + 1) + (-1) ^ (k + 1)) + 2 * (2 ^ k + (-1) ^ k) := by rw [IH1, IH2]
_ = (2 : ℤ) ^ (k + 2) + (-1) ^ (k + 2) := by ring
6.3.2. Example
Problem
Prove that for all natural numbers \(m\geq 1\), \(a_m\) is congruent to either 1 or 5 modulo 6.
Solution
We will prove a more precise result than stated, namely that for all natural numbers \(n\geq 1\), either
\(a_n\equiv 1\mod 6\) and \(a_{n+1}\equiv 5\mod 6\), or
\(a_n\equiv 5\mod 6\) and \(a_{n+1}\equiv 1\mod 6\).
We prove this by induction on \(n\).
For the base case, \(n=1\), notice that \(a_1=1\) and \(a_2=5\), so \(a_1\equiv 1\mod 6\) and \(a_2\equiv 5\mod 6\).
For the inductive step, let \(k\) be a natural number and suppose that either
\(a_k\equiv 1\mod 6\) and \(a_{k+1}\equiv 5\mod 6\), or
\(a_k\equiv 5\mod 6\) and \(a_{k+1}\equiv 1\mod 6\).
Case 1 (\(a_k\equiv 1\mod 6\) and \(a_{k+1}\equiv 5\mod 6\)): Then
Case 2 (\(a_k\equiv 5\mod 6\) and \(a_{k+1}\equiv 1\mod 6\)): Then
It may not be clear to you exactly why these calculations are what’s needed to solve the problem. There is also quite a bit of low-level logical manipulation happening, without being called out directly in the text. The Lean proof below may make some of these logical manipulations more apparent to you.
example {m : ℕ} (hm : 1 ≤ m) : a m ≡ 1 [ZMOD 6] ∨ a m ≡ 5 [ZMOD 6] := by
have H : ∀ n : ℕ, 1 ≤ n →
(a n ≡ 1 [ZMOD 6] ∧ a (n + 1) ≡ 5 [ZMOD 6])
∨ (a n ≡ 5 [ZMOD 6] ∧ a (n + 1) ≡ 1 [ZMOD 6])
· intro n hn
induction_from_starting_point n, hn with k hk IH
· left
constructor
calc a 1 = 1 := by rw [a]
_ ≡ 1 [ZMOD 6] := by extra
calc a (1 + 1) = 1 + 2 * 2 := by rw [a, a, a]
_ = 5 := by numbers
_ ≡ 5 [ZMOD 6] := by extra
· obtain ⟨IH1, IH2⟩ | ⟨IH1, IH2⟩ := IH
· right
constructor
· apply IH2
calc a (k + 1 + 1) = a (k + 1) + 2 * a k := by rw [a]
_ ≡ 5 + 2 * 1 [ZMOD 6] := by rel [IH1, IH2]
_ = 6 * 1 + 1 := by numbers
_ ≡ 1 [ZMOD 6] := by extra
· left
constructor
· apply IH2
calc a (k + 1 + 1) = a (k + 1) + 2 * a k := by rw [a]
_ ≡ 1 + 2 * 5 [ZMOD 6] := by rel [IH1, IH2]
_ = 6 * 1 + 5 := by numbers
_ ≡ 5 [ZMOD 6] := by extra
obtain ⟨H1, H2⟩ | ⟨H1, H2⟩ := H m hm
· left
apply H1
· right
apply H1
6.3.3. Example
The most famous example of a sequence defined recursively in terms of its two previous values is the Fibonacci sequence: each term is the sum of the two previous.
def F : ℕ → ℤ
| 0 => 1
| 1 => 1
| n + 2 => F (n + 1) + F n
Work out the first 10 terms, on paper or with Lean’s help.
Problem
Show that the Fibonacci sequence \((F_n)\) satisfies: for all natural numbers \(n\), \(F_n \le 2^n\).
Solution
We prove this by induction on \(n\).
For \(n=0\), we have that
For \(n=1\), we have that
Let \(k\) be a natural number and suppose that \(F_k\le 2^k\) and \(F_{k+1}\le 2^{k+1}\). Then
example (n : ℕ) : F n ≤ 2 ^ n := by
two_step_induction n with k IH1 IH2
· calc F 0 = 1 := by rw [F]
_ ≤ 2 ^ 0 := by numbers
· calc F 1 = 1 := by rw [F]
_ ≤ 2 ^ 1 := by numbers
· calc F (k + 2) = F (k + 1) + F k := by rw [F]
_ ≤ 2 ^ (k + 1) + 2 ^ k := by rel [IH1, IH2]
_ ≤ 2 ^ (k + 1) + 2 ^ k + 2 ^ k := by extra
_ = 2 ^ (k + 2) := by ring
6.3.4. Example
Problem
Show 1 that the Fibonacci sequence \((F_n)\) satisfies: for all natural numbers \(n\),
Solution
We prove this by induction on \(n\). First,
Now, let \(k\) be a natural number and suppose that \(F_{k+1}^2-F_{k+1}F_k-F_k^2=-(-1)^k\). Then
example (n : ℕ) : F (n + 1) ^ 2 - F (n + 1) * F n - F n ^ 2 = - (-1) ^ n := by
simple_induction n with k IH
· calc F 1 ^ 2 - F 1 * F 0 - F 0 ^ 2 = 1 ^ 2 - 1 * 1 - 1 ^ 2 := by rw [F, F]
_ = - (-1) ^ 0 := by numbers
· calc F (k + 2) ^ 2 - F (k + 2) * F (k + 1) - F (k + 1) ^ 2
= (F (k + 1) + F k) ^ 2 - (F (k + 1) + F k) * F (k + 1)
- F (k + 1) ^ 2 := by rw [F]
_ = - (F (k + 1) ^ 2 - F (k + 1) * F k - F k ^ 2) := by ring
_ = - -(-1) ^ k := by rw [IH]
_ = -(-1) ^ (k + 1) := by ring
6.3.5. Example
We have so far seen simple induction, induction from a specified starting point, and two-step induction. It may not surprise you to learn that it is also valid to perform two-step induction from a specified starting point.
Consider the sequence \((d_n)\) defined recursively by,
\[\begin{split}d_0&=3\\ d_1&=1\\ \text{for }n:\mathbb{N},\quad d_{n+2}&=3d_{n+1}+5d_n.\end{split}\]
def d : ℕ → ℤ
| 0 => 3
| 1 => 1
| k + 2 => 3 * d (k + 1) + 5 * d k
Problem
Show that for all sufficiently large natural numbers \(n\), \(d_n \ge 4^n\).
To start this problem, you might experiment by calculating the first few terms, by hand or in Lean.
#eval d 2 -- infoview displays `18`
#eval d 3 -- infoview displays `59`
#eval d 4 -- infoview displays `267`
#eval d 5 -- infoview displays `1096`
#eval d 6 -- infoview displays `4623`
#eval d 7 -- infoview displays `19349`
Likewise, you can calculate the first few powers of 4, by hand or in Lean.
#eval 4 ^ 2 -- infoview displays `16`
#eval 4 ^ 3 -- infoview displays `64`
#eval 4 ^ 4 -- infoview displays `256`
#eval 4 ^ 5 -- infoview displays `1024`
#eval 4 ^ 6 -- infoview displays `4096`
#eval 4 ^ 7 -- infoview displays `16384`
Based on this limited sample, it looks like \(d_n\) overtakes \(4^n\) at \(n=4\). So let’s try an induction starting at 4.
Solution
We will show this for all natural numbers \(n\geq 4\).
For \(n=4\), we have that
For \(n=5\), we have that
Let \(k\) be a natural number and suppose that \(d_k\ge 4^k\) and \(d_{k+1}\ge 4^{k+1}\). Then we have that
In Lean, we can use the tactic two_step_induction_from_starting_point for this style of
argument.
example : forall_sufficiently_large n : ℕ, d n ≥ 4 ^ n := by
dsimp
use 4
intro n hn
two_step_induction_from_starting_point n, hn with k hk IH1 IH2
· calc d 4 = 267 := by rfl
_ ≥ 4 ^ 4 := by numbers
· calc d 5 = 1096 := by rfl
_ ≥ 4 ^ 5 := by numbers
calc d (k + 2) = 3 * d (k + 1) + 5 * d k := by rw [d]
_ ≥ 3 * 4 ^ (k + 1) + 5 * 4 ^ k := by rel [IH1, IH2]
_ = 16 * 4 ^ k + 4 ^ k := by ring
_ ≥ 16 * 4 ^ k := by extra
_ = 4 ^ (k + 2) := by ring
6.3.6. Exercises
Consider the sequence \((b_n)\) defined recursively by,
\[\begin{split}b_0&=0\\ b_1&=1\\ \text{for }n:\mathbb{N},\quad b_{n+2}&=5b_{n+1}-6b_n.\end{split}\]Prove that for all natural numbers \(n\), \(b_n=3^n - 2 ^ n\).
def b : ℕ → ℤ | 0 => 0 | 1 => 1 | n + 2 => 5 * b (n + 1) - 6 * b n example (n : ℕ) : b n = 3 ^ n - 2 ^ n := by sorry
Consider the sequence \((c_n)\) defined recursively by,
\[\begin{split}c_0&=3\\ c_1&=2\\ \text{for }n:\mathbb{N},\quad c_{n+2}&=4c_n.\end{split}\]Prove that for all natural numbers \(n\), \(c_n=2\cdot 2^n+(-2)^n\).
def c : ℕ → ℤ | 0 => 3 | 1 => 2 | n + 2 => 4 * c n example (n : ℕ) : c n = 2 * 2 ^ n + (-2) ^ n := by sorry
Consider the sequence \((t_n)\) defined recursively by,
\[\begin{split}t_0&=5\\ t_1&=7\\ \text{for }n:\mathbb{N},\quad t_{n+2}&=2t_{n+1}-t_n.\end{split}\]Prove that for all natural numbers \(n\), \(t_n=2n+5\).
def t : ℕ → ℤ | 0 => 5 | 1 => 7 | n + 2 => 2 * t (n + 1) - t n example (n : ℕ) : t n = 2 * n + 5 := by sorry
Consider the sequence \((q_n)\) defined recursively by,
\[\begin{split}q_0&=1\\ q_1&=2\\ \text{for }n:\mathbb{N},\quad q_{n+2}&=2q_{n+1}-q_n+6n + 6.\end{split}\]Prove that for all natural numbers \(n\), \(q_n=n^3+1\).
def q : ℕ → ℤ | 0 => 1 | 1 => 2 | n + 2 => 2 * q (n + 1) - q n + 6 * n + 6 example (n : ℕ) : q n = (n:ℤ) ^ 3 + 1 := by sorry
Consider the sequence \((s_n)\) defined recursively by,
\[\begin{split}s_0&=2\\ s_1&=3\\ \text{for }n:\mathbb{N},\quad s_{n+2}&=2s_{n+1}+3s_n.\end{split}\]Prove that for all natural numbers \(m\), \(s_m\) is congruent to either 2 or 3 modulo 5.
def s : ℕ → ℤ | 0 => 2 | 1 => 3 | n + 2 => 2 * s (n + 1) + 3 * s n example (m : ℕ) : s m ≡ 2 [ZMOD 5] ∨ s m ≡ 3 [ZMOD 5] := by sorry
Consider the sequence \((p_n)\) defined recursively by,
\[\begin{split}p_0&=2\\ p_1&=3\\ \text{for }n:\mathbb{N},\quad p_{n+2}&=6p_{n+1}-p_n.\end{split}\]Prove that for all natural numbers \(m\geq 1\), \(p_m\) is congruent to either 2 or 3 modulo 7.
def p : ℕ → ℤ | 0 => 2 | 1 => 3 | n + 2 => 6 * p (n + 1) - p n example (m : ℕ) : p m ≡ 2 [ZMOD 7] ∨ p m ≡ 3 [ZMOD 7] := by sorry
Consider the sequence \((r_n)\) defined recursively by,
\[\begin{split}r_0&=2\\ r_1&=0\\ \text{for }n:\mathbb{N},\quad r_{n+2}&=2r_{n+1}+r_n.\end{split}\]Prove that for all sufficiently large natural numbers \(n\), it is true that \(r_n\geq 2^n\).
def r : ℕ → ℤ | 0 => 2 | 1 => 0 | n + 2 => 2 * r (n + 1) + r n example : forall_sufficiently_large n : ℕ, r n ≥ 2 ^ n := by sorry
Show that the Fibonacci sequence \((F_n)\) satisfies: for all sufficiently large natural numbers \(n\), \(0.4 \cdot 1.6^n < F_n < 0.5 \cdot 1.7^n\).
example : forall_sufficiently_large n : ℕ, (0.4:ℚ) * 1.6 ^ n < F n ∧ F n < (0.5:ℚ) * 1.7 ^ n := by sorry
Footnotes
- 1
Example adapted from Hammack, Book of Proof, Section 10.5.
6.4. Strong induction
6.4.1. Example
We have been encountering increasingly complicated induction principles, starting from “simple induction” in Example 6.1.1 and eventually reaching rather niche induction principles like “two-step induction from a specified starting point” in Example 6.3.5. Rather than develop more and more exotic induction principles as our problems become yet more complicated, let’s explain a more general method: strong induction. This method lets us prove a proposition for the natural numbers one by one, relying at each step not just on the immediately previous step, but on any previous step.
Let’s re-do Example 6.3.3 using strong induction. The differences will be more apparent in Lean, but we start with a text proof, where the difference amounts to a change of emphasis.
Problem
Show that for all natural numbers \(n\), \(F_n \le 2^n\).
Solution
We prove this by strong induction on \(n\). Let \(n\) be a natural number and suppose that for all natural numbers \(m < n\), \(F_m \le 2^m\). \((\star)\)
We consider cases according to whether \(n\) is 0, 1, or \(k + 2\) for some natural number \(k\).
For \(n=0\), we have that
For \(n=1\), we have that
For \(n=k+2\), we have that \(k<k+2\) and \(k+1<k+2\), so by the inductive hypothesis \((\star)\), \(F_k\le 2^k\) and \(F_{k+1}\le 2^{k+1}\). Thus
In Lean, strong induction can be used in a proof almost silently. We set up a theorem stating the result we want to prove by strong induction (here the statement
for all natural numbers \(n\), \(F_n \le 2^n\)
which I have named F_bound in Lean). Then within the proof of that theorem we can refer to the
theorem itself! Lean will attempt to check for us that we are using the theorem only for input
values smaller than the value currently being studied.
You might find this suspicious, or in danger of becoming circular. Check for yourself that if you
try to invoke the lemma F_bound at the value \(n\) itself, or at a larger value like
\(n + 17\), then Lean gives an error.
theorem F_bound (n : ℕ) : F n ≤ 2 ^ n := by
match n with
| 0 =>
calc F 0 = 1 := by rw [F]
_ ≤ 2 ^ 0 := by numbers
| 1 =>
calc F 1 = 1 := by rw [F]
_ ≤ 2 ^ 1 := by numbers
| k + 2 =>
have IH1 := F_bound k -- first inductive hypothesis
have IH2 := F_bound (k + 1) -- second inductive hypothesis
calc F (k + 2) = F (k + 1) + F k := by rw [F]
_ ≤ 2 ^ (k + 1) + 2 ^ k := by rel [IH1, IH2]
_ ≤ 2 ^ (k + 1) + 2 ^ k + 2 ^ k := by extra
_ = 2 ^ (k + 2) := by ring
6.4.2. Example
Theorem
Let \(n \geq 2\) be a natural number. Then there exists a prime number \(p\) which is a factor of \(n\).
Proof
We prove this by strong induction on \(n\). Let \(n\) be a natural number and suppose that for all natural numbers \(2 \le m < n\), there exists a prime number \(p\) which is a factor of \(m\). \((\star)\)
If \(n\) is prime, then \(n\) itself is a prime factor of \(n\), and we are done.
If \(n\) is not prime, then since \(n \geq 2\), there exists a natural number \(2 \le m < n\) which is a factor of \(n\). (This was proved in one of the exercises in Section 5.3.) By the inductive hypothesis \((\star)\), there exists a prime number \(p\) which is a factor of \(m\).
Since \(m\mid n\), there exists a natural number \(x\) such that \(n = mx\). Since \(p \mid m\), there exists a natural number \(y\) such that \(m = py\). Then
so \(p\) is a factor of \(n\) too.
Here is the same proof in Lean. The lemma from the exercise in
Section 5.3 has the Lean name exists_factor_of_not_prime.
Notice that this is again a strong induction proof: we are invoking the theorem (which we name
exists_prime_factor), instantiated for \(m\), within the proof of the theorem instantiated
for \(n\). At that point Lean has a hypothesis available saying that \(m<n\), so this is
valid.
theorem exists_prime_factor {n : ℕ} (hn2 : 2 ≤ n) : ∃ p : ℕ, Prime p ∧ p ∣ n := by
by_cases hn : Prime n
. -- case 1: `n` is prime
use n
constructor
· apply hn
· use 1
ring
. -- case 2: `n` is not prime
obtain ⟨m, hmn, _, ⟨x, hx⟩⟩ := exists_factor_of_not_prime hn hn2
have IH : ∃ p, Prime p ∧ p ∣ m := exists_prime_factor hmn -- inductive hypothesis
obtain ⟨p, hp, y, hy⟩ := IH
use p
constructor
· apply hp
· use x * y
calc n = m * x := hx
_ = (p * y) * x := by rw [hy]
_ = p * (x * y) := by ring
6.4.3. Exercises
Show that for all natural numbers \(n>0\), there exist natural numbers \(a\) and \(x\), with \(x\) odd, such that \(n=2^ax\).
Suggested approach: start with a case split on the parity of \(n\), using the lemma
even_or_odd.theorem extract_pow_two (n : ℕ) (hn : 0 < n) : ∃ a x, Odd x ∧ n = 2 ^ a * x := by sorry
6.5. Pascal’s triangle
6.5.1. Definition
Consider the family of natural numbers \((P_{a,b})\) defined recursively by,
\[\begin{split}\text{for }a:\mathbb{N},\quad P_{a,0}&=1 \\ \text{for }b:\mathbb{N},\quad P_{0,b+1}&=1 \\ \text{for }a,b:\mathbb{N},\quad P_{a+1,b+1} &= P_{a+1,b}+P_{a,b+1}.\end{split}\]
This definition is well-founded because each step of the definition depends only on previous terms \(P_{a,b}\) for which the expression \(a+b\) is strictly smaller.
Here is how this looks in Lean, with the well-foundedness explanation expressed using the syntax
termination_by.
def pascal : ℕ → ℕ → ℕ
| a, 0 => 1
| 0, b + 1 => 1
| a + 1, b + 1 => pascal (a + 1) b + pascal a (b + 1)
termination_by _ a b => a + b
As usual, Lean can work out any value of the function we ask for. For example,
#eval pascal 2 4 -- infoview displays `15`
Here are all the values for \(a\) and \(b\) from 0 to 5.
0 |
1 |
2 |
3 |
4 |
5 |
|
|---|---|---|---|---|---|---|
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
2 |
3 |
4 |
5 |
6 |
2 |
1 |
3 |
6 |
10 |
15 |
21 |
3 |
1 |
4 |
10 |
20 |
35 |
56 |
4 |
1 |
5 |
15 |
35 |
70 |
126 |
5 |
1 |
6 |
21 |
56 |
126 |
252 |
Check your understanding of the definition by re-calculating a few of these values from scratch.
The conventional visualization of the function pascal is in a rotated version of the above
table, as a triangle.
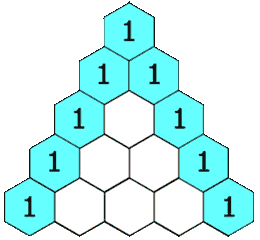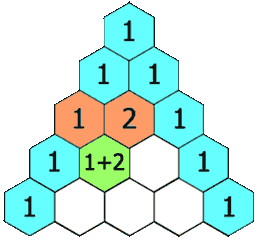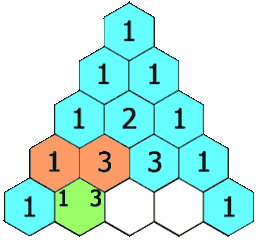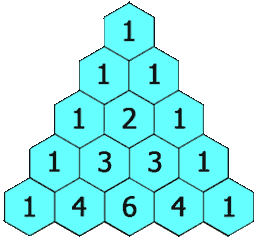
Fig. 6.1 Pascal’s triangle (image credit: Wikimedia Commons)
6.5.2. Example
Theorem
For all natural numbers \(a\) and \(b\), \(P_{a,b} \le (a+b)!\).
Proof
We prove this by strong induction relative to the expression \(a+b\).
By an exercise in Section 6.2, factorials are always \(\geq 1\), so for all \(a\),
and for all \(b\),
Now let \(a\) and \(b\) be natural numbers and suppose that for all \(x\) and \(y\) with \(x+y<(a+1)+(b+1)\), it is true that \(P_{x,y} \le (x+y)!\). Then in particular
So
theorem pascal_le (a b : ℕ) : pascal a b ≤ (a + b)! := by
match a, b with
| a, 0 =>
calc pascal a 0 = 1 := by rw [pascal]
_ ≤ (a + 0)! := by apply factorial_pos
| 0, b + 1 =>
calc pascal 0 (b + 1) = 1 := by rw [pascal]
_ ≤ (0 + (b + 1))! := by apply factorial_pos
| a + 1, b + 1 =>
have IH1 := pascal_le (a + 1) b -- inductive hypothesis
have IH2 := pascal_le a (b + 1) -- inductive hypothesis
calc pascal (a + 1) (b + 1) = pascal (a + 1) b + pascal a (b + 1) := by rw [pascal]
_ ≤ (a + 1 + b) ! + (a + (b + 1)) ! := by rel [IH1, IH2]
_ ≤ (a + b) * (a + b + 1) ! + (a + 1 + b) ! + (a + (b + 1)) ! := by extra
_ = ((a + b + 1) + 1) * (a + b + 1)! := by ring
_ = ((a + b + 1) + 1)! := by rw [factorial, factorial, factorial]
_ = (a + 1 + (b + 1))! := by ring
termination_by _ a b => a + b
6.5.3. Example
With a more delicate calculation, we can improve the bound in Example 6.5.2 to an exact formula.
Theorem
For all natural numbers \(a\) and \(b\), \(P_{a,b} \ a! \ b!= (a+b)!\).
Proof
We prove this by strong induction relative to the expression \(a+b\).
For all \(a\),
and for all \(b\),
Now let \(a\) and \(b\) be natural numbers and suppose that for all \(x\) and \(y\) with \(x+y<(a+1)+(b+1)\), it is true that \(P_{x,y} \ x! \ y! = (x+y)!\). Then in particular
So
theorem pascal_eq (a b : ℕ) : pascal a b * a ! * b ! = (a + b)! := by
match a, b with
| a, 0 =>
calc pascal _ 0 * a ! * 0! = 1 * a ! * 0! := by rw [pascal]
_ = 1 * a ! * 1 := by rw [factorial]
_ = (a + 0)! := by ring
| 0, b + 1 =>
calc pascal 0 (b + 1) * 0 ! * (b + 1)! = 1 * 0 ! * (b + 1)! := by rw [pascal]
_ = 1 * 1 * (b + 1)! := by rw [factorial, factorial]
_ = (0 + (b + 1))! := by ring
| a + 1, b + 1 =>
have IH1 := pascal_eq (a + 1) b -- inductive hypothesis
have IH2 := pascal_eq a (b + 1) -- inductive hypothesis
calc
pascal (a + 1) (b + 1) * (a + 1)! * (b + 1)!
= (pascal (a + 1) b + pascal a (b + 1)) * (a + 1)! * (b + 1)! := by rw [pascal]
_ = pascal (a + 1) b * (a + 1)! * (b + 1)!
+ pascal a (b + 1) * (a + 1)! * (b + 1)! := by ring
_ = pascal (a + 1) b * (a + 1)! * ((b + 1) * b !)
+ pascal a (b + 1) * ((a + 1) * a !) * (b + 1)! := by rw [factorial, factorial]
_ = (b + 1) * (pascal (a + 1) b * (a + 1)! * b !)
+ (a + 1) * (pascal a (b + 1) * a ! * (b + 1)!) := by ring
_ = (b + 1) * ((a + 1) + b) !
+ (a + 1) * (a + (b + 1)) ! := by rw [IH1, IH2]
_ = ((1 + a + b) + 1) * (1 + a + b) ! := by ring
_ = ((1 + a + b) + 1) ! := by rw [factorial]
_ = ((a + 1) + (b + 1)) ! := by ring
termination_by _ a b => a + b
Corollary
For all natural numbers \(a\) and \(b\),
This fact is a trivial rearrangement of the theorem above, but the Lean proof is more complicated,
due to issues with division, which in this book we largely avoid. Don’t sweat the details here,
or the two unfamiliar tactics field_simp and norm_cast.
example (a b : ℕ) : (pascal a b : ℚ) = (a + b)! / (a ! * b !) := by
have ha := factorial_pos a
have hb := factorial_pos b
field_simp [ha, hb]
norm_cast
calc pascal a b * (a ! * b !) = pascal a b * a ! * b ! := by ring
_ = (a + b)! := by apply pascal_eq
6.5.4. Exercises
Prove that for all natural numbers \(a\) and \(b\), \(P_{a,b} =P_{b,a}\).
theorem pascal_symm (m n : ℕ) : pascal m n = pascal n m := by match m, n with | 0, 0 => sorry | a + 1, 0 => sorry | 0, b + 1 => sorry | a + 1, b + 1 => sorry termination_by _ a b => a + b
Prove using simple induction that for all natural numbers \(a\), \(P_{a,1} =a+1\).
example (a : ℕ) : pascal a 1 = a + 1 := by sorry
6.6. The Division Algorithm
6.6.1. Definition
Consider the functions \(\operatorname{mod}\) and \(\operatorname{div}\) defined recursively on the integers by,
The idea will be that \(\operatorname{div}\) computes the quotient of \(n\) by \(d\) (in the elementary-school sense where we produce an integer rather than continuing into decimal places), and \(\operatorname{mod}\) computes the remainder of \(n\) on division by \(d\). For example,
These definitions are well-founded because each step of the definition depends only on previous terms \(\operatorname{mod}(n, d)\), \(\operatorname{div}(n, d)\) for which the expression \(2n - d\) is strictly smaller in absolute value. (This is not very obvious, although Lean can prove it automatically. As a sanity check,
which decreases strictly.) Here is how this looks in Lean, with the well-foundedness explanation
expressed using the syntax termination_by, as in Definition 6.5.1.
def fmod (n d : ℤ) : ℤ :=
if n * d < 0 then
fmod (n + d) d
else if h2 : 0 < d * (n - d) then
fmod (n - d) d
else if h3 : n = d then
0
else
n
termination_by _ n d => 2 * n - d
def fdiv (n d : ℤ) : ℤ :=
if n * d < 0 then
fdiv (n + d) d - 1
else if 0 < d * (n - d) then
fdiv (n - d) d + 1
else if h3 : n = d then
1
else
0
termination_by _ n d => 2 * n - d
Let’s check they do what they’re supposed to:
#eval fmod 11 4 -- infoview displays `3`
#eval fdiv 11 4 -- infoview displays `2`
Compute a few examples yourself (checking your work with Lean) and see if you believe that \(\operatorname{div}\) and \(\operatorname{mod}\) are producing “quotient” and “remainder”. Now let’s make that rigorous.
6.6.2. Example
Theorem
For any integers \(n\) and \(d\), we have that \(\operatorname{mod}(n, d) + d \cdot \operatorname{div}(n, d) = n\).
Proof
We prove this by strong induction relative to the expression \(2n - d\). Suppose that for all integers \(m\) and \(c\) with \(|2m - c|<|2n-d|\), it is true that \(\operatorname{mod}(n, d) + d \cdot \operatorname{div}(n, d) = n\).
Case 1 (\(nd<0\)): Then by the inductive hypothesis
so
Case 2 (\(0<d(n-d)\)): Then by the inductive hypothesis
so
Case 3 (\(n=d\)): Then
Case 4: In this case,
theorem fmod_add_fdiv (n d : ℤ) : fmod n d + d * fdiv n d = n := by
rw [fdiv, fmod]
split_ifs with h1 h2 h3 <;> push_neg at *
· -- case `n * d < 0`
have IH := fmod_add_fdiv (n + d) d -- inductive hypothesis
calc fmod (n + d) d + d * (fdiv (n + d) d - 1)
= (fmod (n + d) d + d * fdiv (n + d) d) - d := by ring
_ = (n + d) - d := by rw [IH]
_ = n := by ring
· -- case `0 < d * (n - d)`
have IH := fmod_add_fdiv (n - d) d -- inductive hypothesis
calc fmod (n - d) d + d * (fdiv (n - d) d + 1)
= (fmod (n - d) d + d * fdiv (n - d) d) + d := by ring
_ = n := by addarith [IH]
· -- case `n = d`
calc 0 + d * 1 = d := by ring
_ = n := by rw [h3]
· -- last case
ring
termination_by _ n d => 2 * n - d
6.6.3. Example
Theorem
For any integers \(n\) and \(d\), with \(d\) positive, we have that \(\operatorname{mod}(n, d)\) is nonnegative.
Proof
We prove this by strong induction relative to the expression \(2n - d\). Suppose that for all integers \(m\) and \(c\) with \(c\) positive and \(|2m - c|<|2n-d|\), it is true that \(\operatorname{mod}(m, c)\) is nonnegative.
Case 1 (\(nd<0\)): Then by the inductive hypothesis \(\operatorname{mod}(n, d)=\operatorname{mod}(n + d, d)\geq 0\).
Case 2 (\(0<d(n-d)\)): Then by the inductive hypothesis \(\operatorname{mod}(n, d)=\operatorname{mod}(n - d, d)\geq 0\).
Case 3 (\(n=d\)): Then \(\operatorname{mod}(n, d)= 0\), so \(\operatorname{mod}(n, d)\geq 0\).
Case 4 (\(0\le nd\le d^2\) and \(n\ne d\)): Then since \(0\le nd\) and by hypothesis \(0<d\), we have that \(\operatorname{mod}(n, d)=n\geq 0\).
theorem fmod_nonneg_of_pos (n : ℤ) {d : ℤ} (hd : 0 < d) : 0 ≤ fmod n d := by
rw [fmod]
split_ifs with h1 h2 h3 <;> push_neg at *
· -- case `n * d < 0`
have IH := fmod_nonneg_of_pos (n + d) hd -- inductive hypothesis
apply IH
· -- case `0 < d * (n - d)`
have IH := fmod_nonneg_of_pos (n - d) hd -- inductive hypothesis
apply IH
· -- case `n = d`
extra
· -- last case
cancel d at h1
termination_by _ n d hd => 2 * n - d
6.6.4. Example
Theorem
For any integers \(n\) and \(d\), with \(d\) positive, we have that \(\operatorname{mod}(n, d)<d\).
Proof
We prove this by strong induction relative to the expression \(2n - d\). Suppose that for all integers \(m\) and \(c\) with \(c\) positive and \(|2m - c|<|2n-d|\), it is true that \(\operatorname{mod}(m, c)<c\).
Case 1 (\(nd<0\)): Then by the inductive hypothesis \(\operatorname{mod}(n, d)=\operatorname{mod}(n + d, d)<d\).
Case 2 (\(0<d(n-d)\)): Then by the inductive hypothesis \(\operatorname{mod}(n, d)=\operatorname{mod}(n - d, d)<d\).
Case 3 (\(n=d\)): Then \(\operatorname{mod}(n, d)= 0<d\) by hypothesis.
Case 4 (\(0\le nd\le d^2\) and \(n\ne d\)): We have that \(n-d\le 0\), since \(d(n-d)\le 0\) and by hypothesis \(0<d\). Therefore \(n\le d\). Also, by hypothesis, \(n\ne d\). Combining these, we have that \(n< d\).
theorem fmod_lt_of_pos (n : ℤ) {d : ℤ} (hd : 0 < d) : fmod n d < d := by
rw [fmod]
split_ifs with h1 h2 h3 <;> push_neg at *
· -- case `n * d < 0`
have IH := fmod_lt_of_pos (n + d) hd -- inductive hypothesis
apply IH
· -- case `0 < d * (n - d)`
have IH := fmod_lt_of_pos (n - d) hd -- inductive hypothesis
apply IH
· -- case `n = d`
apply hd
· -- last case
have h4 :=
calc 0 ≤ - d * (n - d) := by addarith [h2]
_ = d * (d - n) := by ring
cancel d at h4
apply lt_of_le_of_ne
· addarith [h4]
· apply h3
termination_by _ n d hd => 2 * n - d
6.6.5. Example
Putting this all together, we can prove the following theorem. This theorem justifies the tactic
mod_cases, which we have been using since Example 3.4.4: we can list out
just finitely many possibilities for an integer \(a\), considered modulo a positive integer
\(b\).
Theorem
Let \(a\) and \(b\) be integers, with \(b\) positive. There exists an integer \(r\), with \(0 \le r < b\), such that \(a \equiv r\mod b\).
Proof
We will show that the integer \(\operatorname{mod}(a,b)\) has this property. Indeed, by Example 6.6.3 and Example 6.6.4, \(0 \le \operatorname{mod}(a,b) < b\), and by Example 6.6.2,
so
so
example (a b : ℤ) (h : 0 < b) : ∃ r : ℤ, 0 ≤ r ∧ r < b ∧ a ≡ r [ZMOD b] := by
use fmod a b
constructor
· apply fmod_nonneg_of_pos a h
constructor
· apply fmod_lt_of_pos a h
· use fdiv a b
have Hab : fmod a b + b * fdiv a b = a := fmod_add_fdiv a b
addarith [Hab]
6.6.6. Exercises
Prove the analogue of Example 6.6.4 for \(d\) negative: For any integers \(n\) and \(d\), with \(d\) negative, we have that \(d<\operatorname{mod}(n, d)\).
theorem lt_fmod_of_neg (n : ℤ) {d : ℤ} (hd : d < 0) : d < fmod n d := by sorry
Consider the function \(T\) defined recursively on the integers by,
\[\begin{split}T(n)= \begin{cases} T(1-n)+2n-1,&0< n\\ T(-n),&n< 0\\ 0&n=0. \end{cases}\end{split}\]This recursive definition is well-founded, since its self-references are strictly decreasing in \(|3n-1|\).
Prove that for all integers \(n\), \(T(n)=n^2\).
def T (n : ℤ) : ℤ := if 0 < n then T (1 - n) + 2 * n - 1 else if 0 < - n then T (-n) else 0 termination_by T n => 3 * n - 1 theorem T_eq (n : ℤ) : T n = n ^ 2 := by sorry
Let \(a\) and \(b\) be integers, with \(b\) positive. Prove that there exists a unique integer \(r\) in the range \(0 \le r < b\), such that \(a\equiv r\mod b\).
This theorem is an upgrade to Example 6.6.5, stating uniqueness as well as existence. We stated it without proof in Example 4.3.4 (with the Lean name
Int.existsUnique_modEq_lt) and have been implicitly using it whenever we deduce a contradiction involving “obvious non-congruences”, such as in Example 4.4.3.Suggested approach: Write the following as a stand-alone theorem
uniquenessand prove it, somewhat along the lines of the special case proved in Example 4.3.4:Let \(a\) and \(b\) be integers, with \(b\) positive. Let \(r\) and \(s\) be integers, both in the range \(0 \le r < b\), \(0 \le s < b\) and both congruent to \(a\) modulo \(b\). Show that they are equal.
Then put all the pieces together, combining that with the argument from Example 6.6.5.
theorem uniqueness (a b : ℤ) (h : 0 < b) {r s : ℤ} (hr : 0 ≤ r ∧ r < b ∧ a ≡ r [ZMOD b]) (hs : 0 ≤ s ∧ s < b ∧ a ≡ s [ZMOD b]) : r = s := by sorry example (a b : ℤ) (h : 0 < b) : ∃! r : ℤ, 0 ≤ r ∧ r < b ∧ a ≡ r [ZMOD b] := by sorry
6.7. The Euclidean algorithm
6.7.1. Definition
Definition
The function \(\operatorname{gcd}\) of two integers is defined recursively as follows:
\[\begin{split}\operatorname{gcd}(a,b)= \begin{cases} \operatorname{gcd}(b,\operatorname{mod}(a,b)) & 0< b\\ \operatorname{gcd}(b,\operatorname{mod}(a,-b)) & b< 0\\ a & b=0\text{ and }0\le a\\ -a & b=0\text{ and }a<0. \end{cases}\end{split}\]
Let’s practice evaluating the \(\operatorname{gcd}\) function. We calculate \(\operatorname{gcd}(-21,15)\):
(Remember that \(\operatorname{mod}(a,b)\) is the “remainder” function, defined in Definition 6.6.1.)
As in Definition 6.5.1 and Definition 6.6.1, we need to justify that this recursive definition is well-founded, that is that the process always terminates. And as in those sections, we do this by providing an expression which becomes strictly smaller in absolute value as the process goes on. Here that expression is \(b\), the second of the two numbers (note that in the example we have \(b\) being successively 15, 9, 6, 3, 0, which indeed is decreasing.)
This leads to the following attempt at a Lean definition for \(\operatorname{gcd}\), with the
clause termination_by _ a b => b indicating that \(b\) is the size expression for the
well-foundedness.
def gcd (a b : ℤ) : ℤ :=
if 0 < b then
gcd b (fmod a b)
else if b < 0 then
gcd b (fmod a (-b))
else if 0 ≤ a then
a
else
-a
termination_by _ a b => b
But unlike in Section 6.5 and Section 6.6, the definition is not yet complete: the fact that \(b\) is decreasing along the recursion is “non-obvious enough” that it requires an explicit proof.
Proposition
The recursive definition \(\operatorname{gcd}\) is well-founded.
Proof
There are two things to check:
\(\underline{\text{If }0<b\text{ then }-b<\operatorname{mod}(a,b)<b}\): By Example 6.6.3 and Example 6.6.4, \(0\le \operatorname{mod}(a,b)<b\), which establishes the upper bound immediately and the lower bound since
\[\begin{split}-b&<0\\ &\le \operatorname{mod}(a,b).\end{split}\]\(\underline{\text{If }b<0\text{ then }b<\operatorname{mod}(a,-b)<-b}\): We have that \(0<-b\), so by Example 6.6.3 and Example 6.6.4, \(0\le \operatorname{mod}(a,-b)<-b\), which establishes the upper bound immediately and the lower bound since
\[\begin{split}b&<0\\ &\le \operatorname{mod}(a,-b).\end{split}\]
In Lean, we state and prove these facts separately, tagging them with the attribute
@[decreasing], which lets the subsequent definition gcd call on them for the
well-foundedness. Check that if they are omitted then the definition gives an error.
@[decreasing] theorem lower_bound_fmod1 (a b : ℤ) (h1 : 0 < b) : -b < fmod a b := by
have H : 0 ≤ fmod a b
· apply fmod_nonneg_of_pos
apply h1
calc -b < 0 := by addarith [h1]
_ ≤ _ := H
@[decreasing] theorem lower_bound_fmod2 (a b : ℤ) (h1 : b < 0) : b < fmod a (-b) := by
have H : 0 ≤ fmod a (-b)
· apply fmod_nonneg_of_pos
addarith [h1]
have h2 : 0 < -b := by addarith [h1]
calc b < 0 := h1
_ ≤ fmod a (-b) := H
@[decreasing] theorem upper_bound_fmod2 (a b : ℤ) (h1 : b < 0) : fmod a (-b) < -b := by
apply fmod_lt_of_pos
addarith [h1]
@[decreasing] theorem upper_bound_fmod1 (a b : ℤ) (h1 : 0 < b) : fmod a b < b := by
apply fmod_lt_of_pos
apply h1
After this the Lean definition gcd goes through successfully. Sanity check: does the Lean
definition agree with our calculation above for \(\operatorname{gcd}(-21,15)\)?
#eval gcd (-21) 15 -- infoview displays `3`
6.7.2. Example
Every fact about \(\operatorname{gcd}\) will be proved by strong induction, using the same well-foundedness justification.
Proposition
For all integers \(a\) and \(b\), the integer \(\operatorname{gcd}(a,b)\) is nonnegative.
Proof
We prove this by strong induction on \(b\). Suppose that for all integers \(x\) and \(y\) with \(|y|<|b|\), it is true that \(0 \le \operatorname{gcd}(x, y)\).
Case 1 (\(0<b\)): Then \(\operatorname{gcd}(a,b)\) is equal to \(\operatorname{gcd}(b,\operatorname{mod}(a,b))\) which by the inductive hypothesis is nonnegative.
Case 2 (\(b<0\)): Then \(\operatorname{gcd}(a,b)\) is equal to \(\operatorname{gcd}(b,\operatorname{mod}(a,-b))\) which by the inductive hypothesis is nonnegative.
Case 3 (\(b=0\), \(0\le a\)): Then we have that \(\operatorname{gcd}(a,b)=a\geq 0\).
Case 4 (\(b=0\), \(a<0\)): Then we have that \(\operatorname{gcd}(a,b)=-a\geq 0\).
theorem gcd_nonneg (a b : ℤ) : 0 ≤ gcd a b := by
rw [gcd]
split_ifs with h1 h2 ha <;> push_neg at *
· -- case `0 < b`
have IH := gcd_nonneg b (fmod a b) -- inductive hypothesis
apply IH
· -- case `b < 0`
have IH := gcd_nonneg b (fmod a (-b)) -- inductive hypothesis
apply IH
· -- case `b = 0`, `0 ≤ a`
apply ha
· -- case `b = 0`, `a < 0`
addarith [ha]
termination_by _ a b => b
6.7.3. Example
Proposition
For all integers \(a\) and \(b\), the integer \(\operatorname{gcd}(a,b)\) is a factor of both \(a\) and \(b\).
That is, \(\operatorname{gcd}(a,b)\) is a common divisor of \(a\) and \(b\). We will prove later (see the exercises) that in fact it is the greatest common divisor of \(a\) and \(b\), hence the acronym GCD.
Proof
We prove this by strong induction on \(b\). Suppose that for all integers \(x\) and \(y\) with \(|y|<|b|\), it is true that \(0 \le \operatorname{gcd}(x, y)\).
Case 1 (\(0<b\)): Let \(q=\operatorname{div}(a,b)\) and let \(r=\operatorname{mod}(a,b)\), so that \(a=r+bq\) (by Example 6.6.2).
Then by the recursive definition \(\operatorname{gcd}(a,b)\) is equal to \(\operatorname{gcd}(b,r)\), and by the inductive hypothesis this divides both \(b\) and \(r\). We need to show it divides \(b\) (which is immediate) and \(a\), which we now turn to.
Since \(\operatorname{gcd}(a,b)\mid b\), there exists an integer \(k\) such that \(b = \operatorname{gcd}(a,b)k\), and since \(\operatorname{gcd}(a,b)\mid r\), there exists an integer \(l\) such that \(r = \operatorname{gcd}(a,b)l\). We now have
so \(\operatorname{gcd}(a,b)\mid a\).
Case 2 (\(b<0\)): Let \(q=\operatorname{div}(a,-b)\) and let \(r=\operatorname{mod}(a,-b)\), so that \(a=r+(-b)q\) (by Example 6.6.2).
Then by the recursive definition \(\operatorname{gcd}(a,b)\) is equal to \(\operatorname{gcd}(b,r)\), and by the inductive hypothesis this divides both \(b\) and \(r\). We need to show it divides \(b\) (which is immediate) and \(a\), which we now turn to.
Since \(\operatorname{gcd}(a,b)\mid b\), there exists an integer \(k\) such that \(b = \operatorname{gcd}(a,b)k\), and since \(\operatorname{gcd}(a,b)\mid r\), there exists an integer \(l\) such that \(r = \operatorname{gcd}(a,b)l\). We now have
so \(\operatorname{gcd}(a,b)\mid a\).
Case 3 (\(b=0\), \(0\le a\)): Then we have that \(\operatorname{gcd}(a,b)=a\), which is a factor of \(a\) since \(a\cdot 1=a\) and \(b\) since
Case 4 (\(b=0\), \(a<0\)): Then we have that \(\operatorname{gcd}(a,b)=-a\), which is a factor of \(a\) since \(-a\cdot -1=a\) and \(b\) since
It would be possible to set up this proof in Lean with the structure of an “and” goal, like this:
(The _ are placeholders just to show the basic structure.)
theorem gcd_dvd (a b : ℤ) : gcd a b ∣ b ∧ gcd a b ∣ a := by
rw [gcd]
split_ifs with h1 h2 <;> push_neg at *
· -- case `0 < b`
have IH : _ ∧ _ := gcd_dvd b (fmod a b) -- inductive hypothesis
obtain ⟨IH_right, IH_left⟩ := IH
constructor
· -- prove that `gcd a b ∣ b`
sorry
· -- prove that `gcd a b ∣ a`
sorry
· -- case `b < 0`
have IH : _ ∧ _ := gcd_dvd b (fmod a (-b)) -- inductive hypothesis
obtain ⟨IH_right, IH_left⟩ := IH
constructor
· -- prove that `gcd a b ∣ b`
sorry
· -- prove that `gcd a b ∣ a`
sorry
· -- case `b = 0`, `0 ≤ a`
constructor
· -- prove that `gcd a b ∣ b`
sorry
· -- prove that `gcd a b ∣ a`
sorry
· -- case `b = 0`, `a < 0`
constructor
· -- prove that `gcd a b ∣ b`
sorry
· -- prove that `gcd a b ∣ a`
sorry
termination_by gcd_dvd a b => b
But the constant switching between the \(\operatorname{gcd}(a,b)\mid b\) task and the \(\operatorname{gcd}(a,b)\mid a\) task is a little hard to keep track of. A more elegant setup features two separate lemmas, one to show \(\operatorname{gcd}(a,b)\mid b\) and one to show \(\operatorname{gcd}(a,b)\mid a\), with the following structure:
theorem gcd_dvd_right (a b : ℤ) : gcd a b ∣ b := by
rw [gcd]
split_ifs with h1 h2 <;> push_neg at *
· -- case `0 < b`
have IH := gcd_dvd_left b (fmod a b) -- inductive hypothesis
· -- case `b < 0`
have IH := gcd_dvd_left b (fmod a (-b)) -- inductive hypothesis
· -- case `b = 0`, `0 ≤ a`
sorry
· -- case `b = 0`, `a < 0`
sorry
theorem gcd_dvd_left (a b : ℤ) : gcd a b ∣ a := by
rw [gcd]
split_ifs with h1 h2 <;> push_neg at *
· -- case `0 < b`
have IH1 := gcd_dvd_left b (fmod a b) -- inductive hypothesis
have IH2 := gcd_dvd_right b (fmod a b) -- inductive hypothesis
sorry
· -- case `b < 0`
have IH1 := gcd_dvd_left b (fmod a (-b)) -- inductive hypothesis
have IH2 := gcd_dvd_right b (fmod a (-b)) -- inductive hypothesis
sorry
· -- case `b = 0`, `0 ≤ a`
sorry
· -- case `b = 0`, `a < 0`
sorry
But now the strong induction structure is complicated: the proof of gcd_dvd_right depends on
gcd_dvd_left for smaller values of a, b, and the proof of gcd_dvd_left depends on
gcd_dvd_right for smaller values of a, b. This is called a mutual induction and it
has a special syntax in Lean: the two theorems are enclosed in a mutual block, with a joint
termination explanation at the end, like this:
mutual
theorem gcd_dvd_right (a b : ℤ) : gcd a b ∣ b := by
...
theorem gcd_dvd_left (a b : ℤ) : gcd a b ∣ a := by
...
end
termination_by gcd_dvd_right a b => b ; gcd_dvd_left a b => b
Here is the full proof in Lean.
mutual
theorem gcd_dvd_right (a b : ℤ) : gcd a b ∣ b := by
rw [gcd]
split_ifs with h1 h2 <;> push_neg at *
· -- case `0 < b`
apply gcd_dvd_left b (fmod a b) -- inductive hypothesis
· -- case `b < 0`
apply gcd_dvd_left b (fmod a (-b)) -- inductive hypothesis
· -- case `b = 0`, `0 ≤ a`
have hb : b = 0 := le_antisymm h1 h2
use 0
calc b = 0 := hb
_ = a * 0 := by ring
· -- case `b = 0`, `a < 0`
have hb : b = 0 := le_antisymm h1 h2
use 0
calc b = 0 := hb
_ = -a * 0 := by ring
theorem gcd_dvd_left (a b : ℤ) : gcd a b ∣ a := by
rw [gcd]
split_ifs with h1 h2 <;> push_neg at *
· -- case `0 < b`
have IH1 := gcd_dvd_left b (fmod a b) -- inductive hypothesis
have IH2 := gcd_dvd_right b (fmod a b) -- inductive hypothesis
obtain ⟨k, hk⟩ := IH1
obtain ⟨l, hl⟩ := IH2
have H : fmod a b + b * fdiv a b = a := fmod_add_fdiv a b
set q := fdiv a b
set r := fmod a b
use l + k * q
calc a = r + b * q := by rw [H]
_ = gcd b r * l + (gcd b r * k) * q := by rw [← hk, ← hl]
_ = gcd b r * (l + k * q) := by ring
· -- case `b < 0`
have IH1 := gcd_dvd_left b (fmod a (-b)) -- inductive hypothesis
have IH2 := gcd_dvd_right b (fmod a (-b)) -- inductive hypothesis
obtain ⟨k, hk⟩ := IH1
obtain ⟨l, hl⟩ := IH2
have H := fmod_add_fdiv a (-b)
set q := fdiv a (-b)
set r := fmod a (-b)
use l - k * q
calc a = r + (-b) * q := by rw [H]
_ = gcd b r * l + (- (gcd b r * k)) * q := by rw [← hk, ← hl]
_ = gcd b r * (l - k * q) := by ring
· -- case `b = 0`, `0 ≤ a`
use 1
ring
· -- case `b = 0`, `a < 0`
use -1
ring
end
termination_by gcd_dvd_right a b => b ; gcd_dvd_left a b => b
There is a new tactic in the above proof: set, which introduce a short name for a long
expression (typically one which occurs frequently and you are tired of typing out in full). Notice
how the goal state changes before and after its use.
6.7.4. Definition
The process described in Definition 6.7.1 is generally called the Euclidean algorithm. A process called the extended Euclidean algorithm is used to compute two other functions, which we will call \(L(a,b)\) and \(R(a,b)\), at the same time as \(\operatorname{gcd}(a,b)\).
Definition
The functions \(L\) and \(R\) of two integers are defined mutually recursively as follows:
\[\begin{split}L(a,b)&= \begin{cases} R(b,\operatorname{mod}(a,b)) & 0< b\\ R(b,\operatorname{mod}(a,-b)) & b<0\\ 1 & b=0\text{ and }0\le a\\ -1 & b=0\text{ and }a <0. \end{cases} \\ R(a,b)&= \begin{cases} L(b,\operatorname{mod}(a,b))-\operatorname{div}(a,b)R(b,\operatorname{mod}(a,b)) & 0< b\\ L(b,\operatorname{mod}(a,-b))+\operatorname{div}(a,-b)R(b,\operatorname{mod}(a,-b)) & b<0\\ 0 & b=0. \end{cases} \\\end{split}\]
Let’s practice evaluating the \(\operatorname{gcd}(a,b)\), \(L(a,b)\) and \(R(a,b)\) functions jointly, on the same example (\(a=-21\), \(b=15\)) as in Definition 6.7.1.
Since we will need both \(\operatorname{div}\) and \(\operatorname{mod}\) down the recursion, it is convenient to calculate them jointly in advance:
(This table is a shorthand record that \(\operatorname{div}(-21,15)=-2\) and \(\operatorname{mod}(-21,15)=9\), and so on.) We conclude immediately that
as before. To calculate \(L(a,b)\) and \(R(a,b)\), it is convenient to work backwards:
In Lean this mutual-recursion definition looks similar to the mutual-induction proof in
Example 6.7.3; like that example it is enclosed in a block marked
mutual.
mutual
def L (a b : ℤ) : ℤ :=
if 0 < b then
R b (fmod a b)
else if b < 0 then
R b (fmod a (-b))
else if 0 ≤ a then
1
else
-1
def R (a b : ℤ) : ℤ :=
if 0 < b then
L b (fmod a b) - (fdiv a b) * R b (fmod a b)
else if b < 0 then
L b (fmod a (-b)) + (fdiv a (-b)) * R b (fmod a (-b))
else
0
end
termination_by L a b => b ; R a b => b
Sanity check: does the Lean definition agree with our computation by hand of \(L(-21,15)\) and \(R(-21,15)\)?
#eval L (-21) 15 -- infoview displays `2`
#eval R (-21) 15 -- infoview displays `3`
6.7.5. Example
The reason for making the definitions \(L(a,b)\) and \(R(a,b)\) is that they satisfy the following identity.
Theorem
For all integers \(a\) and \(b\),
Proof
We prove this by strong induction on \(b\). Suppose that for all integers \(x\) and \(y\) with \(|y|<|b|\), it is true that \(0 \le \operatorname{gcd}(x, y)\).
Case 1 (\(0<b\)): Let \(q=\operatorname{div}(a,b)\) and let \(r=\operatorname{mod}(a,b)\), so that \(a=r+bq\) (by Example 6.6.2).
Then by the recurrence definitions,
and by the inductive hypothesis \(L(b,r)b+R(b,r)r=\operatorname{gcd}(b,r)\). So
Case 2 (\(b<0\)): Let \(q=\operatorname{div}(a,-b)\) and let \(r=\operatorname{mod}(a,-b)\), so that \(a=r+(-b)q\) (by Example 6.6.2).
Then by the recurrence definitions,
and by the inductive hypothesis \(L(b,r)b+R(b,r)r=\operatorname{gcd}(b,r)\). So
Case 3 (\(b=0\), \(0\le a\)): Then by the recurrence definitions, \(\operatorname{gcd}(a,b)=a\), \(L(a,b)=1\) and \(R(a,b)=0\), so
Case 4 (\(b=0\), \(a<0\)): Then by the recurrence definitions, \(\operatorname{gcd}(a,b)=-a\), \(L(a,b)=-1\) and \(R(a,b)=0\), so
Here is the same proof in Lean.
theorem L_mul_add_R_mul (a b : ℤ) : L a b * a + R a b * b = gcd a b := by
rw [R, L, gcd]
split_ifs with h1 h2 <;> push_neg at *
· -- case `0 < b`
have IH := L_mul_add_R_mul b (fmod a b) -- inductive hypothesis
have H : fmod a b + b * fdiv a b = a := fmod_add_fdiv a b
set q := fdiv a b
set r := fmod a b
calc R b r * a + (L b r - q * R b r) * b
= R b r * (r + b * q) + (L b r - q * R b r) * b:= by rw [H]
_ = L b r * b + R b r * r := by ring
_ = gcd b r := IH
· -- case `b < 0`
have IH := L_mul_add_R_mul b (fmod a (-b)) -- inductive hypothesis
have H : fmod a (-b) + (-b) * fdiv a (-b) = a := fmod_add_fdiv a (-b)
set q := fdiv a (-b)
set r := fmod a (-b)
calc R b r * a + (L b r + q * R b r) * b
= R b r * (r + -b * q) + (L b r + q * R b r) * b := by rw [H]
_ = L b r * b + R b r * r := by ring
_ = gcd b r := IH
· -- case `b = 0`, `0 ≤ a`
ring
· -- case `b = 0`, `a < 0`
ring
termination_by L_mul_add_R_mul a b => b
6.7.6. Example
We proved in Example 6.7.5 that for any integers \(a\) and \(b\), the integers \(L(a,b)\) and \(R(a,b)\) satisfy
For example, \(L(7,5)=-2\) and \(R(7,5)=3\) and \(\operatorname{gcd}(7,5)=1\)
#eval L 7 5 -- infoview displays `-2`
#eval R 7 5 -- infoview displays `3`
#eval gcd 7 5 -- infoview displays `1`
and \((-2) \cdot 7 + 3 \cdot 5 = 1\).
But it is interesting to note that these are generally not the only pair of integers with that property. For example,
In applications, it is common to need only the property, not the particular construction via \(L(a,b)\) and \(R(a,b)\). So we record this separately. This fact is known as Bézout’s identity.
Corollary (Bézout’s identity)
Let \(a\) and \(b\) be integers. Then there exist integers \(x\) and \(y\), such that \(xa+yb=\operatorname{gcd}(a,b)\).
Proof
By Example 6.7.5, the integers \(L(a,b)\) and \(R(a,b)\) have this property.
theorem bezout (a b : ℤ) : ∃ x y : ℤ, x * a + y * b = gcd a b := by
use L a b, R a b
apply L_mul_add_R_mul
6.7.7. Exercises
Show that \(\operatorname{gcd}(a,b)\) is not just a common divisor of \(a\) and \(b\) (see Example 6.7.3), but their greatest common divisor: if \(d\) is an integer which divides both \(a\) and \(b\), then it divides \(\operatorname{gcd}(a,b)\).
This problem does not need an induction; it is a direct corollary of Bézout’s identity (Example 6.7.6).
theorem gcd_maximal {d a b : ℤ} (ha : d ∣ a) (hb : d ∣ b) : d ∣ gcd a b := by sorry