8. Functions
So far in the book, we have studied properties of numbers (whether a number is odd, positive, prime; whether one number is divisible by another) and operations on numbers (addition, greatest common divisor).
In this chapter we go up a level of abstraction, and study properties of and operations on functions. These new properties include: whether a function is injective, surjective, bijective; whether one function is inverse to another; and the operation of composition.
We also expand our horizon beyond the numeric types (\(\mathbb{N}\), \(\mathbb{Z}\), \(\mathbb{Q}\), \(\mathbb{R}\)) which have formed the setting of the early part of the book. We now start to work with a broader range of types, including function types, finite inductive types, and product types.
8.1. Injectivity and surjectivity
8.1.1. Example
We have studied particular functions before. For example, the Fibonacci sequence from Example 6.3.3 is a function from \(\mathbb{N}\) to \(\mathbb{Z}\): it takes in a natural number, for example 5, and gives out an integer, in this case 8 (the index-5 term of the sequence).
def F : ℕ → ℤ
| 0 => 1
| 1 => 1
| n + 2 => F (n + 1) + F n
#eval F 5 -- infoview displays `8`
The domain of a function is the type where it takes its input values, and the codomain of a
function is the type where it takes its output values. For example, the domain of the Fibonacci
sequence is \(\mathbb{N}\) and its codomain is \(\mathbb{Z}\). The type of functions with
domain \(\mathbb{N}\) and codomain \(\mathbb{Z}\) is denoted
\(\mathbb{N}\to \mathbb{Z}\). Lean will confirm for us that the Fibonacci sequence F has
this type:
#check @F -- infoview displays `F : ℕ → ℤ`
Another way to define a function is by a closed formula. For example, “let \(q:\mathbb{R}\to \mathbb{R}\) be the function defined by, \(q(x)=x+3\).” In Lean we can write this as
def q (x : ℝ) : ℝ := x + 3
This function has domain \(\mathbb{R}\) and codomain \(\mathbb{R}\) – I even said when I was defining it that I was making \(q\) to have type \(\mathbb{R}\to \mathbb{R}\). Let’s check that this is indeed the type of the Lean object:
#check @q -- infoview displays `q : ℝ → ℝ`
A third way to define a function, if we expect to use it just once and don’t want to waste a name on it, is by using the notation \(\mapsto\): we can refer to “the function \(x \mapsto x ^ 2\) from \(\mathbb{R}\) to \(\mathbb{R}\)”. Here is the same notation in Lean:
#check fun (x : ℝ) ↦ x ^ 2 -- infoview displays `fun x ↦ x ^ 2 : ℝ → ℝ`
8.1.2. Definition
Now that we have the notation \(X\to Y\) for “the type of functions from \(X\) to \(Y\)”, we can introduce properties of functions, in the same way that we have previously introduced properties (like “odd” and “prime”) of numbers. Here is our first one.
Definition
A function \(f : X \to Y\) is injective, if for all \(x_1\) and \(x_2\) of type \(X\), if \(f(x_1)=f(x_2)\), then \(x_1=x_2\).
def Injective (f : X → Y) : Prop := ∀ {x1 x2 : X}, f x1 = f x2 → x1 = x2
8.1.3. Example
Problem
Show that the function \(q:\mathbb{R}\to\mathbb{R}\) from Example 8.1.1 is injective.
Solution
Let \(x_1\) and \(x_2\) be real numbers and suppose that \(q(x_1)=q(x_2)\). Then \(x_1+1=x_2+1\), so \(x_1=x_2\).
Here is this solution in Lean. Note that after unfolding the definition “injective” using the
command dsimp [Injective], the goal state displays
⊢ ∀ ⦃x1 x2 : ℝ⦄, q x1 = q x2 → x1 = x2
This is the “injective” definition specialized to the problem at hand.
example : Injective q := by
dsimp [Injective]
intro x1 x2 h
dsimp [q] at h
addarith [h]
8.1.4. Example
Problem
Show that the function \(x \mapsto x ^ 2\) from \(\mathbb{R}\) to \(\mathbb{R}\) is not injective.
Solution
We must show that there exist real numbers \(x_1\) and \(x_2\), such that \(x_1{}^2=x_2{}^2\) and \(x_1\ne x_2\). Indeed, -1 and 1 have these properties.
The first sentence of that proof was a negation-normalization: I unfolded the “injective” definition
and restated its negation in a logically equivalent but more convenient form. Recall that in Lean
we do this using the tactic push_neg. Here is the goal state after the tactic push_neg has
been used:
⊢ ∃ x1 x2, x1 ^ 2 = x2 ^ 2 ∧ x1 ≠ x2
And here is the full Lean proof.
example : ¬ Injective (fun x : ℝ ↦ x ^ 2) := by
dsimp [Injective]
push_neg
use -1, 1
constructor
· numbers
· numbers
8.1.5. Definition
Definition
A function \(f : X \to Y\) is surjective, if for all \(y\) of type \(Y\), there exists \(x\) of type \(X\), such that \(f(x)=y\).
def Surjective (f : X → Y) : Prop := ∀ y : Y, ∃ x : X, f x = y
8.1.6. Example
Problem
Consider the function \(s:\mathbb{Q}\to\mathbb{Q}\) defined by, \(s(a)=3a+2\). Show that \(s\) is surjective.
Solution
Let \(y\) be a rational number. Then
Here is the solution in Lean. The goal state after unfolding the definition of “surjective” is
⊢ ∀ (y : ℚ), ∃ x, s x = y
which confirms what we need to prove and why what we wrote in the text proof above is sufficient.
def s (a : ℚ) : ℚ := 3 * a + 2
example : Surjective s := by
dsimp [Surjective]
intro y
use (y - 2) / 3
calc s ((y - 2) / 3) = 3 * ((y - 2) / 3) + 2 := by rw [s]
_ = y := by ring
8.1.7. Example
Problem
Show that the function \(x \mapsto x ^ 2\) from \(\mathbb{R}\) to \(\mathbb{R}\) is not surjective.
Solution
We will show that there exists a real number \(y\), such that for all real numbers \(x\), \(x^2\ne y\).
Indeed, let us show that -1 has this property. Let \(x\) be a real number. Then
so \(x^2\ne -1\).
As in Example 8.1.4, the first sentence constitutes a
negation-normalization of the definition of “surjective” in this context. Effectively we are stating
what would be the goal state in the Lean proof after push_neg.
⊢ ∃ y, ∀ (x : ℝ), x ^ 2 ≠ y
And here is the full Lean proof.
example : ¬ Surjective (fun x : ℝ ↦ x ^ 2) := by
dsimp [Surjective]
push_neg
use -1
intro x
apply ne_of_gt
calc -1 < 0 := by numbers
_ ≤ x ^ 2 := by extra
8.1.8. Example
We have so far seen numeric types, like the integers \(\mathbb{Z}\) and the real numbers \(\mathbb{R}\), and function types, like \(\mathbb{Z}\to \mathbb{R}\) (the functions from \(\mathbb{Z}\) to \(\mathbb{R}\)).
Another way to make a type is as a finite set of options. Finite types are useful for conceptual examples, because everything is explicit and checkable.
inductive Musketeer
| athos
| porthos
| aramis
deriving DecidableEq
Here is how to define a function whose domain is a given finite inductive type.
def f : Musketeer → Musketeer
| athos => aramis
| porthos => aramis
| aramis => athos
Problem
Show that the function \(f\) is not injective.
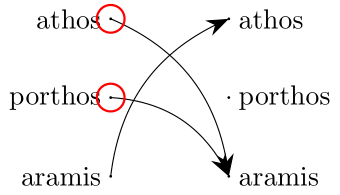
example : ¬ Injective f := by
dsimp [Injective]
push_neg
use athos, porthos
dsimp [f] -- optional
exhaust
The tactic exhaust is new here. At the place where it is used, the goal state is
aramis = aramis ∧ athos ≠ porthos
that is,
True ∧ ¬ False
which is logically equivalent to True. The tactic exhaust can do this kind of propositional
logic reasoning, up to arbitrary complexity.
In particular, exhaust can prove any (true) variable-free statement in an inductive type, and
that’s how we’ll use it in this chapter. We start making more serious use of exhaust in
Chapter 9.
8.1.9. Example
Problem
Show that the function \(f\) defined in Example 8.1.8 is not surjective.
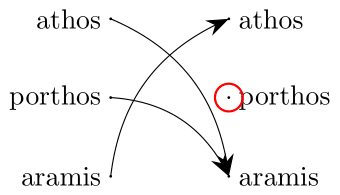
We can case-check on a variable a in a finite inductive type using the tactic cases.
example : ¬ Surjective f := by
dsimp [Surjective]
push_neg
use porthos
intro a
cases a
· exhaust
· exhaust
· exhaust
Such proofs can become repetitive, and you may wish to use a trick we have seen before (for example
Example 4.4.4, Example 4.5.9,
Example 6.6.2, Example 6.7.2): when a tactic such as
cases generates many goals which can all be proved by the same tactic, you can write
<;> to apply the tactic to all those goals.
-- better (more automated) version of the previous proof
example : ¬ Surjective f := by
dsimp [Surjective]
push_neg
use porthos
intro a
cases a <;> exhaust
You might also like to check that the cases a <;> exhaust line is necessary; exhaust can’t close
the goal on its own. As discussed in Example 8.1.8, exhaust can prove any
(true) variable-free statement in an inductive type, but before the cases a <;> exhaust line the
goal state is
a : Musketeer
⊢ f a ≠ porthos
which contains a variable, a.
8.1.10. Example
Let \(g\) be the following function from the Musketeer type to itself:
def g : Musketeer → Musketeer
| athos => porthos
| porthos => aramis
| aramis => athos
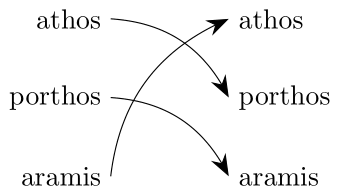
Problem
Show that the function \(g\) is injective.
There are a lot of cases in this proof – \(3 \times 3 = 9\), to be precise. Fortunately
exhaust can prove all of them!
example : Injective g := by
dsimp [Injective]
intro x1 x2 hx
cases x1 <;> cases x2 <;> exhaust
8.1.11. Example
Problem
Show that the function \(g\) defined in Example 8.1.10 is surjective.
example : Surjective g := by
dsimp [Surjective]
intro y
cases y
· use aramis
exhaust
· use athos
exhaust
· use porthos
exhaust
8.1.12. Example
We finish with a relatively hard example. The proof here is efficient and self-contained but not particularly well-motivated. For an alternative (perhaps more intuitive) approach, combine the last exercise in this section (the one about strictly monotone functions) with the idea from Example 2.1.8.
Problem
Show that the function \(x \mapsto x ^ 3\) from \(\mathbb{R}\) to \(\mathbb{R}\) is injective.
Solution
Let \(x_1\) and \(x_2\) be real numbers and suppose that \(x_1{}^3=x_2{}^3\). Then
so either \(x_1-x_2=0\), in which case we are done, or \(x_1{}^2+x_1x_2+x_2{}^2=0\), which we henceforth assume.
We now consider a further case split according to whether \(x_1=0\).
Case 1 (\(x_1=0\)): Then
so \(x_2=0\) also. Thus \(x_1=0=x_2\) as required.
Case 2 (\(x_1\ne 0\)): Then
contradiction.
example : Injective (fun (x:ℝ) ↦ x ^ 3) := by
intro x1 x2 hx
dsimp at hx
have H : (x1 - x2) * (x1 ^ 2 + x1 * x2 + x2 ^ 2) = 0
· calc (x1 - x2) * (x1 ^ 2 + x1 * x2 + x2 ^ 2) = x1 ^ 3 - x2 ^ 3 := by ring
_ = x1 ^ 3 - x1 ^ 3 := by rw [hx]
_ = 0 := by ring
rw [mul_eq_zero] at H
obtain H1 | H2 := H
· -- case 1: x1 - x2 = 0
addarith [H1]
· -- case 2: x1 ^2 + x1 * x2 + x2 ^ 2 = 0
by_cases hx1 : x1 = 0
· -- case 2a: x1 = 0
have hx2 :=
calc x2 ^ 3 = x1 ^ 3 := by rw [hx]
_ = 0 ^ 3 := by rw [hx1]
_ = 0 := by numbers
cancel 3 at hx2
calc x1 = 0 := by rw [hx1]
_ = x2 := by rw [hx2]
· -- case 2b: x1 ≠ 0
have :=
calc 0 < x1 ^ 2 + ((x1 + x2) ^ 2 + x2 ^ 2) := by extra
_ = 2 * (x1 ^ 2 + x1 * x2 + x2 ^ 2) := by ring
_ = 2 * 0 := by rw [H2]
_ = 0 := by ring
numbers at this -- contradiction!
8.1.13. Exercises
Prove or disprove that the function \(x \mapsto x-12\) from \(\mathbb{Q}\) to \(\mathbb{Q}\) is injective.
(If you think it’s true, prove it, by solving the first version below. If you think it’s false, solve the second version.)
example : Injective (fun (x : ℚ) ↦ x - 12) := by sorry example : ¬ Injective (fun (x : ℚ) ↦ x - 12) := by sorry
Prove or disprove that the function \(x \mapsto 3\) from \(\mathbb{R}\) to \(\mathbb{R}\) is injective.
(If you think it’s true, prove it, by solving the first version below. If you think it’s false, solve the second version.)
example : Injective (fun (x : ℝ) ↦ 3) := by sorry example : ¬ Injective (fun (x : ℝ) ↦ 3) := by sorry
Prove or disprove that the function \(x \mapsto 3x-1\) from \(\mathbb{ℚ}\) to \(\mathbb{ℚ}\) is injective.
(If you think it’s true, prove it, by solving the first version below. If you think it’s false, solve the second version.)
example : Injective (fun (x : ℚ) ↦ 3 * x - 1) := by sorry example : ¬ Injective (fun (x : ℚ) ↦ 3 * x - 1) := by sorry
Prove or disprove that the function \(x \mapsto 3x-1\) from \(\mathbb{Z}\) to \(\mathbb{Z}\) is injective.
(If you think it’s true, prove it, by solving the first version below. If you think it’s false, solve the second version.)
example : Injective (fun (x : ℤ) ↦ 3 * x - 1) := by sorry example : ¬ Injective (fun (x : ℤ) ↦ 3 * x - 1) := by sorry
Prove or disprove that the function \(x \mapsto 2x\) from \(\mathbb{R}\) to \(\mathbb{R}\) is surjective.
(If you think it’s true, prove it, by solving the first version below. If you think it’s false, solve the second version.)
example : Surjective (fun (x : ℝ) ↦ 2 * x) := by sorry example : ¬ Surjective (fun (x : ℝ) ↦ 2 * x) := by sorry
Prove or disprove that the function \(x \mapsto 2x\) from \(\mathbb{Z}\) to \(\mathbb{Z}\) is surjective.
(If you think it’s true, prove it, by solving the first version below. If you think it’s false, solve the second version.)
example : Surjective (fun (x : ℤ) ↦ 2 * x) := by sorry example : ¬ Surjective (fun (x : ℤ) ↦ 2 * x) := by sorry
Prove or disprove that the function \(n \mapsto n^2\) from \(\mathbb{N}\) to \(\mathbb{N}\) is surjective.
(If you think it’s true, prove it, by solving the first version below. If you think it’s false, solve the second version.)
example : Surjective (fun (n : ℕ) ↦ n ^ 2) := by sorry example : ¬ Surjective (fun (n : ℕ) ↦ n ^ 2) := by sorry
Consider the following finite inductive type White, and the following function \(h\) from the Musketeer type (see Example 8.1.8) to the White type. Prove or disprove that the function \(h\) is injective.
(If you think it’s true, prove it, by solving the first version below. If you think it’s false, solve the second version.)
inductive White | meg | jack deriving DecidableEq open White def h : Musketeer → White | athos => jack | porthos => meg | aramis => jack example : Injective h := by sorry example : ¬ Injective h := by sorry
Prove or disprove that the function \(h\) from the previous example is surjective.
(If you think it’s true, prove it, by solving the first version below. If you think it’s false, solve the second version.)
example : Surjective h := by sorry example : ¬ Surjective h := by sorry
Consider the following function \(l\) from the White type (see the previous two problems) to the Musketeer type (see Example 8.1.8). Prove or disprove that the function \(l\) is injective.
(If you think it’s true, prove it, by solving the first version below. If you think it’s false, solve the second version.)
def l : White → Musketeer | meg => aramis | jack => porthos example : Injective l := by sorry example : ¬ Injective l := by sorry
Prove or disprove that the function \(l\) from the previous example is surjective.
(If you think it’s true, prove it, by solving the first version below. If you think it’s false, solve the second version.)
example : Surjective l := by sorry example : ¬ Surjective l := by sorry
Let \(f : X \to Y\) be a function. Show that \(f\) is injective if and only if for all \(x_1\) and \(x_2\) of type \(X\), if \(x_1\ne x_2\) then \(f(x_1)\ne f(x_2)\).
You will need to use a tactic (such as
push_negorby_cases) which is capable of handling the subtler negations.example (f : X → Y) : Injective f ↔ ∀ x1 x2 : X, x1 ≠ x2 → f x1 ≠ f x2 := by sorry
Prove or disprove that for all functions \(f:\mathbb{Q}\to \mathbb{Q}\), if \(f\) is injective, then the function \(x \mapsto f(x)+1\) from \(\mathbb{Q}\) to \(\mathbb{Q}\) is also injective.
example : ∀ (f : ℚ → ℚ), Injective f → Injective (fun x ↦ f x + 1) := by sorry example : ¬ ∀ (f : ℚ → ℚ), Injective f → Injective (fun x ↦ f x + 1) := by sorry
Prove or disprove that for all functions \(f:\mathbb{Q}\to \mathbb{Q}\), if \(f\) is injective, then the function \(x \mapsto f(x)+x\) from \(\mathbb{Q}\) to \(\mathbb{Q}\) is also injective.
example : ∀ (f : ℚ → ℚ), Injective f → Injective (fun x ↦ f x + x) := by sorry example : ¬ ∀ (f : ℚ → ℚ), Injective f → Injective (fun x ↦ f x + x) := by sorry
Prove or disprove that for all functions \(f:\mathbb{Z}\to \mathbb{Z}\), if \(f\) is surjective, then the function \(x \mapsto 2f(x)\) from \(\mathbb{Z}\) to \(\mathbb{Z}\) is also surjective.
example : ∀ (f : ℤ → ℤ), Surjective f → Surjective (fun x ↦ 2 * f x) := by sorry example : ¬ ∀ (f : ℤ → ℤ), Surjective f → Surjective (fun x ↦ 2 * f x) := by sorry
Prove or disprove that for all real numbers \(c\), the function \(x\mapsto cx\) from \(\mathbb{R}\) to \(\mathbb{R}\) is surjective.
example : ∀ c : ℝ, Surjective (fun x ↦ c * x) := by sorry example : ¬ ∀ c : ℝ, Surjective (fun x ↦ c * x) := by sorry
Let \(f:\mathbb{Q}\to\mathbb{Q}\) be a function which is strictly monotone; that is, for all real numbers \(x\) and \(y\) with \(x<y\), it is true that \(f(x)<f(y)\). Prove that \(f\) is injective.
You may wish to use the lemma
lt_trichotomylemma lt_trichotomy (x y : ℚ) : x < y ∨ x = y ∨ x < y :=
which gives a case division on the relative sizes of two real numbers.
example {f : ℚ → ℚ} (hf : ∀ x y, x < y → f x < f y) : Injective f := by sorry
Let \(f:X\to\mathbb{N}\) be a function, let \(x_0\) be of type \(X\) with \(f(x_0)=0\), and let \(i:X\to X\) be a function such that, for all \(x\), \(f(i(x))=f(x)+1\). Show that \(f\) is surjective. I recommend induction.
We record this theorem for future use under the name
surjective_of_intertwining.example {f : X → ℕ} {x0 : X} (h0 : f x0 = 0) {i : X → X} (hi : ∀ x, f (i x) = f x + 1) : Surjective f := by sorry
8.2. Bijectivity
8.2.1. Definition
Definition
A function is bijective, if it is both injective and surjective.
def Bijective (f : X → Y) : Prop := Injective f ∧ Surjective f
8.2.2. Example
Problem
Let \(p:\mathbb{R}\to\mathbb{R}\) be the function defined by, \(p(x)=2x-5\). Show that \(p\) is bijective.
Solution
We must show that \(p\) is injective and surjective.
For the injectivity, let \(x_1\) and \(x_2\) be real numbers and suppose that \(p(x_1)=p(x_2)\). This means that \(2x_1-5=2x_2-5\). So
For the surjectivity, let \(y\) be a real number. Then
def p (x : ℝ) : ℝ := 2 * x - 5
example : Bijective p := by
dsimp [Bijective]
constructor
· dsimp [Injective]
intro x1 x2 hx
dsimp [p] at hx
calc x1 = ((2 * x1 - 5) + 5) / 2 := by ring
_ = ((2 * x2 - 5) + 5) / 2 := by rw [hx]
_ = x2 := by ring
· dsimp [Surjective]
intro y
use (y + 5) / 2
calc p ((y + 5) / 2) = 2 * ((y + 5) / 2) - 5 := by rfl
_ = y := by ring
8.2.3. Example
Problem
Let \(a:\mathbb{R}\to\mathbb{R}\) be the function defined by, \(a(t)=t^3-t\). Show that \(a\) is not bijective.
Solution
We will show that \(a\) is not injective. Indeed, note that \(0\ne 1\) but
def a (t : ℝ) : ℝ := t ^ 3 - t
example : ¬ Bijective a := by
dsimp [Bijective]
push_neg
left
dsimp [Injective]
push_neg
use 0, 1
constructor
· calc a 0 = 0 ^ 3 - 0 := by rfl
_ = 1 ^ 3 - 1 := by numbers
_ = a 1 := by rfl
· numbers
8.2.4. Example
Consider the following finite inductive types Celestial and Subatomic:
inductive Celestial
| sun
| moon
deriving DecidableEq
inductive Subatomic
| proton
| neutron
| electron
deriving DecidableEq
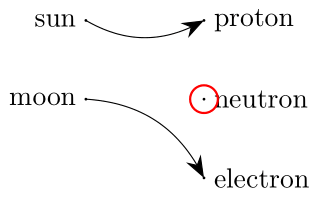
Consider the following function \(f\) from the Celestial type to the Subatomic type.
def f : Celestial → Subatomic
| sun => proton
| moon => electron
Problem
Prove that the function \(f\) is not bijective.
example : ¬ Bijective f := by
dsimp [Bijective]
push_neg
right
dsimp [Surjective]
push_neg
use neutron
intro x
cases x <;> exhaust
8.2.5. Example
Theorem
A function \(f:X\to Y\) is bijective, if and only if for all \(y\) of type \(Y\), there exists a unique \(x\) of type \(X\), such that \(f(x)=y\).
Proof
First, suppose that \(f\) is bijective. Let \(y\) be of type \(Y\). Since \(f\) is surjective, there exists \(x\) of type \(X\), such that \(f(x)=y\). We will show that this \(x\) is unique. Indeed, for any other \(x'\) with \(f(x')=y\), we have that
and so by the injectivity of \(f\), \(x'=x\).
Conversely, suppose that for all \(y\) of type \(Y\), there exists a unique \(x\) of type \(X\), such that \(f(x)=y\). (\(\star\)) We must show that \(f\) is injective and surjective.
For the injectivity, let \(x_1\) and \(x_2\) be of type \(X\), and suppose that \(f(x_1)=f(x_2)\). By (\(\star\)) applied with \(y=f(x_1)\), there exists a unique \(x\) of type \(X\) for which \(f(x)=f(x_1)\). So, by the uniqueness, \(x_1=x\), and also, since \(f(x_2)=f(x_1)=f(x)\), \(x_2=x\). Combining these, \(x_1=x_2\).
For the surjectivity, let \(y\) be of type \(Y\). By (\(\star\)), there exists (a unique) \(x\) of type \(X\) for which \(f(x)=y\).
example {f : X → Y} : Bijective f ↔ ∀ y, ∃! x, f x = y := by
constructor
· -- if `f` is bijective then `∀ y, ∃! x, f x = y`
intro h y
obtain ⟨h_inj, h_surj⟩ := h
obtain ⟨x, hx⟩ := h_surj y
use x
dsimp
constructor
· apply hx
· intro x' hx'
apply h_inj
calc f x' = y := by rw [hx']
_ = f x := by rw [hx]
· -- if `∀ y, ∃! x, f x = y` then `f` is bijective
intro h
constructor
· -- `f` is injective
intro x1 x2 hx1x2
obtain ⟨x, hx, hx'⟩ := h (f x1)
have hxx1 : x1 = x
· apply hx'
rfl
have hxx2 : x2 = x
· apply hx'
rw [hx1x2]
calc x1 = x := by rw [hxx1]
_ = x2 := by rw [hxx2]
· -- `f` is surjective
intro y
obtain ⟨x, hx, hx'⟩ := h y
use x
apply hx
8.2.6. Example
Problem
Show that for all functions \(f\) from the Celestial type (Example 8.2.4) to itself, if \(f\) is injective then it is bijective.
We prove this by an exhaustive analysis of all functions \(f\) from the Celestial type to itself. There are four such functions. I dealt with the first two cases below; fill in the second two cases yourself.
example : ∀ f : Celestial → Celestial, Injective f → Bijective f := by
intro f hf
constructor
· -- `f` is injective by assumption
apply hf
-- show that `f` is surjective
match h_sun : f sun, h_moon : f moon with
| sun, sun =>
have : sun = moon
· apply hf
rw [h_sun, h_moon]
contradiction
| sun, moon =>
intro y
cases y
· use sun
apply h_sun
· use moon
apply h_moon
| moon, sun => sorry
| moon, moon => sorry
8.2.7. Example
Problem
Show that it is not true that for all functions \(f:\mathbb{N}\to \mathbb{N}\), if \(f\) is injective then it is bijective.
Solution
We must show that there exists a function \(f:\mathbb{N}\to \mathbb{N}\), which is injective but not bijective.
Indeed, consider the function \(f(n)=n+1\). This function is injective, since for all natural numbers \(n_1\) and \(n_2\), if \(n_1+1=n_2+1\) then \(n_1=n_2\).
However, this function is not surjective, and therefore not bijective. To see this, observe that for all natural numbers \(n\), we have \(f(n)=n+1>0\) and therefore \(f(n)\ne 0\).
example : ¬ ∀ f : ℕ → ℕ, Injective f → Bijective f := by
push_neg
use fun n ↦ n + 1
constructor
· -- the function is injective
intro n1 n2 hn
addarith [hn]
· -- the function is not bijective
dsimp [Bijective]
push_neg
right
-- specifically, it's not surjective
dsimp [Surjective]
push_neg
use 0
intro n
apply ne_of_gt
extra
8.2.8. Exercises
Prove or disprove that the function \(x \mapsto 4-3x\) from \(\mathbb{R}\) to \(\mathbb{R}\) is bijective.
(If you think it’s true, prove it, by solving the first version below. If you think it’s false, solve the second version.)
example : Bijective (fun (x : ℝ) ↦ 4 - 3 * x) := by sorry example : ¬ Bijective (fun (x : ℝ) ↦ 4 - 3 * x) := by sorry
Prove or disprove that the function \(x \mapsto x^2+2x\) from \(\mathbb{R}\) to \(\mathbb{R}\) is bijective.
(If you think it’s true, prove it, by solving the first version below. If you think it’s false, solve the second version.)
example : Bijective (fun (x : ℝ) ↦ x ^ 2 + 2 * x) := by sorry example : ¬ Bijective (fun (x : ℝ) ↦ x ^ 2 + 2 * x) := by sorry
Consider the following finite inductive type Element, and the following function \(e\) from the Element type to itself. Prove or disprove that the function \(e\) is bijective.
(If you think it’s true, prove it, by solving the first version below. If you think it’s false, solve the second version.)
inductive Element | fire | water | earth | air deriving DecidableEq open Element def e : Element → Element | fire => earth | water => air | earth => fire | air => water example : Bijective e := by sorry example : ¬ Bijective e := by sorry
Show that for all functions \(f\) from the Subatomic type (Example 8.2.4) to itself, if \(f\) is injective then it is bijective.
This is like Example 8.2.6, but with more cases to check.
example : ∀ f : Subatomic → Subatomic, Injective f → Bijective f := by sorry
Consider the finite inductive type Element from a previous exercise. Show that for all functions \(f\) from the Element type to itself, if \(f\) is injective then it is bijective.
This is like Example 8.2.6 and the previous exercise, but with even more (frankly, way too many ….) cases to check.
example : ∀ f : Element → Element, Injective f → Bijective f := by sorry
8.3. Composition of functions
8.3.1. Definition
Definition
The composition of the function \(g : Y \to Z\) with the function \(f : X \to Y\) is the function from \(X\) to \(Z\) which sends \(x\) to \(g(f(x))\).
def comp (f : X → Y) (g : Y → Z) (x : X) : Z := g (f x)
The composition of \(g : Y \to Z\) with \(f : X \to Y\) is denoted \(g \circ f\) (in
Lean, g ∘ f).
8.3.2. Example
Problem
Let \(f:\mathbb{R}\to\mathbb{R}\) be the function defined by, \(f(a)=a+3\). Let \(g:\mathbb{R}\to\mathbb{R}\) be the function defined by, \(g(b)=2b\). Let \(h:\mathbb{R}\to\mathbb{R}\) be the function defined by, \(h(c)=2c+6\).
Show that \(g \circ f = h\).
Solution
Let \(x\) be a real number. Then
In the Lean proof, note the new tactic ext. To prove two functions are equal, we have to
show that they are equal on every input. This is what the tactic ext does. (The name stands
for “extensionality”.) Before we use it, the goal state is
⊢ g ∘ f = h
After we use it, the goal state is
x : ℝ
⊢ (g ∘ f) x = h x
Here is the full Lean proof.
def f (a : ℝ) : ℝ := a + 3
def g (b : ℝ) : ℝ := 2 * b
def h (c : ℝ) : ℝ := 2 * c + 6
example : g ∘ f = h := by
ext x
calc (g ∘ f) x = g (f x) := by rfl
_ = 2 * (x + 3) := by rfl
_ = 2 * x + 6 := by ring
_ = h x := by rfl
8.3.3. Definition
Definition
The identity function \(\operatorname{Id}_X:X\to X\) is the function which sends each \(x\) of type \(X\) to itself.
def id (x : X) : X := x
8.3.4. Example
Problem
Let \(s:\mathbb{R}\to\mathbb{R}\) be the function defined by, \(s(x)=5-x\).
Show that \(s \circ s = \operatorname{Id}_\mathbb{R}\).
Solution
Let \(x\) be a real number. We must show that \(5 - (5 - x) = x\), which is true.
def s (x : ℝ) : ℝ := 5 - x
example : s ∘ s = id := by
ext x
dsimp [s]
ring
8.3.5. Definition
Definition
A function \(g : Y \to X\) is an inverse of \(f : X \to Y\), if \(g \circ f=\operatorname{Id}_X\) and \(f \circ g=\operatorname{Id}_Y\).
def Inverse (f : X → Y) (g : Y → X) : Prop := g ∘ f = id ∧ f ∘ g = id
8.3.6. Example
Consider the following finite inductive type Humour:
inductive Humour
| melancholic
| choleric
| phlegmatic
| sanguine
deriving DecidableEq
Consider the following function \(p\) from the Humour type to itself.
def p : Humour → Humour
| melancholic => choleric
| choleric => sanguine
| phlegmatic => phlegmatic
| sanguine => melancholic
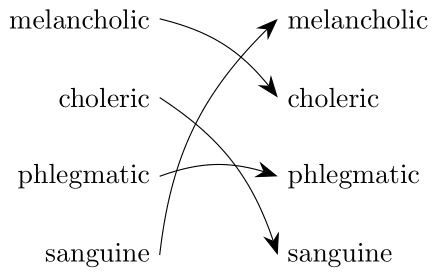
Problem
Define a function \(q\) from the Humour type to itself which is inverse to \(p\), and prove this.
def q : Humour → Humour
| melancholic => sanguine
| choleric => melancholic
| phlegmatic => phlegmatic
| sanguine => choleric
example : Inverse p q := by
constructor
· ext x
cases x <;> exhaust
· ext x
cases x <;> exhaust
8.3.7. Example
Proposition
Let \(f : X \to Y\) be a bijective function. Then there exists a function \(g : Y \to X\) which is inverse to \(f\).
Proof
Define a function \(g : Y \to X\) as follows: given \(y\) of type \(Y\), by the surjectivity of \(f\) there exists an \(x\) of type \(X\) such that \(f(x)=y\), and we set \(g(y)\) to be this \(x\). Thus, for all \(y\), it is true that \(f(g(y))=y\). (\(\star\))
This immediately shows that \(f \circ g = \operatorname{Id}_Y\). To show that \(g \circ f = \operatorname{Id}_X\), let \(x\) be of type \(X\). We have, by (\(\star\)), that
so by the injectivity of \(f\), it follows that \((g \circ f)(x) = \operatorname{Id}_X(x)\).
To write this proof in Lean, we need a tactic, choose, 1 which is not used elsewhere in the
book. This tactic constructs the function \(g : Y \to X\)
as described in the first paragraph of the text proof. More precisely, given the hypothesis
h_surj: ∀ (b : Y), ∃ a, f a = b
the tactic invocation choose g hg using h_surj creates a function consisting of a “choice” of
the a for each b:
g : Y → X
hg : ∀ (b : Y), f (g b) = b
Here is the full proof in Lean.
theorem exists_inverse_of_bijective {f : X → Y} (hf : Bijective f) :
∃ g : Y → X, Inverse f g := by
dsimp [Bijective] at hf
obtain ⟨h_inj, h_surj⟩ := hf
dsimp [Surjective] at h_surj
choose g hg using h_surj
use g
dsimp [Inverse]
constructor
· -- prove `g ∘ f = id`
ext x
dsimp [Injective] at h_inj
apply h_inj
calc f ((g ∘ f) x) = f (g (f x)) := by rfl
_ = f x := by apply hg
_ = f (id x) := by rfl
· -- prove `f ∘ g = id`
ext y
apply hg
8.3.8. Example
Proposition
Let \(f : X \to Y\) and \(g : Y \to X\) be functions, with \(g : Y \to X\) inverse to \(f : X \to Y\). Then \(f : X \to Y\) is bijective.
Proof
We first show \(f\) is injective. Indeed, let \(x_1\) and \(x_2\) be of type \(X\), and suppose that \(f(x_1)=f(x_2)\). Then
We now show that \(f\) is surjective. Indeed, let \(y\) be of type \(Y\). Then
theorem bijective_of_inverse {f : X → Y} {g : Y → X} (h : Inverse f g) :
Bijective f := by
dsimp [Inverse] at h
obtain ⟨hgf, hfg⟩ := h
constructor
· -- `f` is injective
intro x1 x2 hx
calc x1 = id x1 := by rfl
_ = (g ∘ f) x1 := by rw [hgf]
_ = g (f x1) := by rfl
_ = g (f x2) := by rw [hx]
_ = (g ∘ f) x2 := by rfl
_ = id x2 := by rw [hgf]
_ = x2 := by rfl
· -- `f` is surjective
intro y
use g y
calc f (g y) = (f ∘ g) y := by rfl
_ = id y := by rw [hfg]
_ = y := by rfl
8.3.9. Example
Theorem
Let \(f : X \to Y\) be a function. Then \(f\) is bijective, if and only if there exists a function \(g : Y \to X\) which is inverse to \(f\).
Proof
The first direction is given by Example 8.3.7, and the second direction by Example 8.3.8.
theorem bijective_iff_exists_inverse (f : X → Y) :
Bijective f ↔ ∃ g : Y → X, Inverse f g := by
constructor
· apply exists_inverse_of_bijective
· intro h
obtain ⟨g, H⟩ := h
apply bijective_of_inverse H
8.3.10. Exercises
Consider the following functions \(a\) and \(b\) from the Humour type (see Example 8.3.6) to itself. Write down a function \(c\) from the Humour type to itself, so that \(b \circ a=c\).
When you have the right function written down, the included proof will work.
def a : Humour → Humour | melancholic => sanguine | choleric => choleric | phlegmatic => phlegmatic | sanguine => melancholic def b : Humour → Humour | melancholic => phlegmatic | choleric => phlegmatic | phlegmatic => melancholic | sanguine => sanguine def c : Humour → Humour | melancholic => sorry | choleric => sorry | phlegmatic => sorry | sanguine => sorry example : b ∘ a = c := by ext x cases x <;> exhaust
Consider the function \(u:\mathbb{R}\to\mathbb{R}\) defined by, \(u(x)=5x+1\). Write down a function \(v:\mathbb{R}\to\mathbb{R}\) which is inverse to \(u\), and prove it.
def u (x : ℝ) : ℝ := 5 * x + 1 noncomputable def v (x : ℝ) : ℝ := sorry example : Inverse u v := by sorry
Let \(f : X \to Y\) and \(g : Y \to Z\) be injective functions. Show that \(g \circ f\) is also injective.
example {f : X → Y} (hf : Injective f) {g : Y → Z} (hg : Injective g) : Injective (g ∘ f) := by sorry
Let \(f : X \to Y\) and \(g : Y \to Z\) be surjective functions. Show that \(g \circ f\) is also surjective.
example {f : X → Y} (hf : Surjective f) {g : Y → Z} (hg : Surjective g) : Surjective (g ∘ f) := by sorry
Let \(f : X \to Y\) be a surjective function. Show that there exists a function \(g : Y \to Z\), such that \(f \circ g=\operatorname{Id}_Y\).
example {f : X → Y} (hf : Surjective f) : ∃ g : Y → X, f ∘ g = id := by sorry
Let \(f : X \to Y\) and \(g : Y \to X\) be functions, with \(g\) inverse to \(f\). Show that \(f\) is inverse to \(g\).
example {f : X → Y} {g : Y → X} (h : Inverse f g) : Inverse g f := by sorry
Let \(f : X \to Y\) and \(g_1, g_2 : Y \to X\) be functions, with both \(g_1\) and \(g_1\) inverse to \(f\). Show that \(g_1=g_2\).
This problem says that if a function \(f\) has an inverse, then that inverse is unique.
example {f : X → Y} {g1 g2 : Y → X} (h1 : Inverse f g1) (h2 : Inverse f g2) : g1 = g2 := by sorry
Footnotes
- 1
Experts will recognize this as the axiom of choice.
8.4. Product types
8.4.1. Example
Problem
Consider the function \(q:\mathbb{Z}\to\mathbb{Z}^2\) defined by, \(q(m)=(m + 1, 2 - m)\). Show that \(q\) is
injective;
not surjective.
Solution
Let \(m_1\) and \(m_2\) be integers and suppose that \(q(m_1)=q(m_2)\). Then by definition
\[(m_1+1,2-m_1)=(m_2+1,2-m_2),\]so \(m_1+1=m_2+1\) and \(2-m_1=2-m_2\), so \(m_1=m_2\).
We will show that there exists \((a,b)\) in \(\mathbb{Z}^2\) such that for all integers \(m\), \(q(m)\ne(a,b)\). Indeed, we will show that \((0,1)\) has this property. Suppose that \(m\) were an integer with \(q(m)=(0,1)\). Then by definition
\[(m+1,2-m)=(0,1),\]so \(m+1=0\) and \(2-m=1\), hence
\[\begin{split}1&=(m+1)+(2-m)-2\\ &=0+1-2\\ &=-1,\end{split}\]contradiction.
To write these proofs in Lean, notice the use of the tactic obtain in the injectivity problem to
convert the hypothesis of a equality in a product type,
hm : (m1 + 1, 2 - m1) = (m2 + 1, 2 - m2)
to two hypotheses of equality in the two components of the product:
hm' : m1 + 1 = m2 + 1
hm'' : 2 - m1 = 2 - m2
This is consistent with how you should think about equality in a product type: two ordered pairs are equal if the two left parts are equal and the two right parts are equal. So we use the same tactic, with the same syntax, as for the logical operator “and”.
def q (m : ℤ) : ℤ × ℤ := (m + 1, 2 - m)
example : Injective q := by
dsimp [Injective]
intro m1 m2 hm
dsimp [q] at hm
obtain ⟨hm', hm''⟩ := hm
addarith [hm']
The tactic obtain is used similarly in the non-surjectivity problem to break down the hypothesis
of equality in a product type
hm : (m + 1, 2 - m) = (0, 1)
which arises in that problem.
example : ¬ Surjective q := by
dsimp [Surjective]
push_neg
use (0, 1)
intro m hm
dsimp [q] at hm
obtain ⟨hm1, hm2⟩ := hm
have H : 1 = -1 := by addarith [hm1, hm2]
numbers at H
8.4.2. Example
Problem
Consider the function \((m,n)\mapsto (m + n, m + 2n)\) from \(\mathbb{Z}^2\) to \(\mathbb{Z}^2\). Show that this function is bijective.
Usually, the most efficient way to prove a function is bijective is to produce an inverse for it. This is enough because of the theorem we proved in Example 8.3.9. Coming up with this inverse is something you should do in rough work, probably on paper rather than in Lean. For example, in this problem, you can set up an equation in \((a,b)\) which the inverse has to satisfy:
and simplify to a system of integer equations, and then solve for \(m\) and \(n\):
to conclude that a good candidate for the inverse is the function \((a,b)\mapsto (2a-b, b-a)\) from \(\mathbb{Z}^2\) to \(\mathbb{Z}^2\). But this rough work does not get included in the write-up, either on paper or in Lean. Instead, just produce the inverse out of a hat, and check that it works.
Solution
By Example 8.3.9 it suffices to show that this function has an inverse. We will show that the function \((a,b)\mapsto (2a-b, b-a)\) is inverse to this function.
Firstly, for any \((m,n)\) in \(\mathbb{Z}^2\), we have that
Secondly, for any \((a,b)\) in \(\mathbb{Z}^2\), we have that
In Lean, note
the lemma
bijective_iff_exists_inverse, which is the Lean name for the theorem from Example 8.3.9;the use of the tactic
ext(recall Example 8.3.2) to show that two functions are equal by showing that they are equal on arbitrary input.
example : Bijective (fun ((m, n) : ℤ × ℤ) ↦ (m + n, m + 2 * n)) := by
rw [bijective_iff_exists_inverse]
use fun (a, b) ↦ (2 * a - b, b - a)
constructor
· ext ⟨m, n⟩
dsimp
ring
· ext ⟨a, b⟩
dsimp
ring
8.4.3. Example
The ideas of Example 8.4.2 can be adapted fairly flexibly, particularly over the rationals and over the reals. Try this one yourself.
Problem
Consider the function \((m,n)\mapsto (m + n, m - n)\) from \(\mathbb{R}^2\) to \(\mathbb{R}^2\). Show that this function is bijective.
example : Bijective (fun ((m, n) : ℝ × ℝ) ↦ (m + n, m - n)) := by
sorry
But over the integers, complications can ensue. You’ll find that the inverse you come up with for the previous example involves a division, which works fine over \(\mathbb{R}\) but doesn’t work over \(\mathbb{Z}\). And in fact in this case the function is not bijective as a map from \(\mathbb{Z}^2\) to \(\mathbb{Z}^2\).
Problem
Consider the function \((m,n)\mapsto (m + n, m - n)\) from \(\mathbb{Z}^2\) to \(\mathbb{Z}^2\). Show that this function is not bijective.
Solution
We will show that the function is not surjective. In fact, we will show that for all \((m,n)\) in \(\mathbb{Z}^2\), it is not true that \((m + n, m - n)=(0,1)\). So let \((m,n)\) be in \(\mathbb{Z}^2\) and suppose that \((m + n, m - n)=(0,1)\). Then \(m+n=0\) and \(m-n=1\), so
contradiction.
The last part of the problem could play out in several different ways. The hypotheses \(m+n=0\) and \(m-n=1\) are pretty clearly contradictory (for integers), so there are several variant ways you could produce the contradiction instead of the numeric contradiction \(0\equiv 1\mod 2\) which I produced here.
example : ¬ Bijective (fun ((m, n) : ℤ × ℤ) ↦ (m + n, m - n)) := by
dsimp [Bijective, Injective, Surjective]
push_neg
right
use (0, 1)
intro (m, n) h
dsimp at h
obtain ⟨h1, h2⟩ := h
have :=
calc 0 ≡ 2 * m [ZMOD 2] := by extra
_ = (m - n) + (m + n) := by ring
_ = 1 + 0 := by rw [h1, h2]
_ = 1 := by numbers
numbers at this
8.4.4. Example
Problem
Consider the function \((x,y)\mapsto (x+y,x-y, y)\) from \(\mathbb{R}^2\) to \(\mathbb{R}^3\). Show that this function is injective.
Solution
Let \((x_1,y_1)\) and \((x_2,y_2)\) be points in \(\mathbb{R}^2\) and suppose that
Then, inspecting co-ordinate by co-ordinate, we have that
Subtracting the third equation from the first, we also have that \(x_1=x_2\). So \((x_1,y_1)=(x_2,y_2)\).
In Lean, note the use of the tactic constructor to reduce a goal of equality in a product type,
⊢ (x1, y1) = (x2, y2)
to two simpler goals, one for each co-ordinate:
⊢ x1 = x2
⊢ y1 = y2
As with the use of obtain for hypotheses of equality in a product type (recall
Example 8.4.1), the point is that an equality in a product type is
effectively an “and” statement about equality in the first and the second co-ordinates.
example : Injective (fun ((x, y) : ℝ × ℝ) ↦ (x + y, x - y, y)) := by
intro (x1, y1) (x2, y2) h
dsimp at h
obtain ⟨h, h', hy⟩ := h
constructor
· addarith [h, hy]
· apply hy
8.4.5. Example
Problem
Consider the function \((x,y)\mapsto x + y\) from \(\mathbb{R}^2\) to \(\mathbb{R}\). Show that this function is
not injective;
surjective.
Solution
1. We will show that there exist points \((x_1,y_1)\) and \((x_2,y_2)\) in \(\mathbb{R}^2\) such that \(x_1+y_1=x_2+y_2\) and \((x_1,y_1)\ne (x_2,y_2)\). Indeed, consider the points \((0,0)\) and \((1,-1)\). We have that \(0+0=1+-1\) and \((0,0)\ne (1,-1)\).
2. Let \(a\) be a real number. We must show that there exists a point \((x,y)\) in \(\mathbb{R}^2\) such that \(x+y=a\). Indeed, \(a+0=a\), so \((a,0)\) has this property.
example : ¬ Injective (fun ((x, y) : ℝ × ℝ) ↦ x + y) := by
dsimp [Injective]
push_neg
use (0, 0), (1, -1)
dsimp
constructor
· numbers
· numbers
example : Surjective (fun ((x, y) : ℝ × ℝ) ↦ x + y) := by
intro a
use (a, 0)
dsimp
ring
8.4.6. Example
Problem
Consider the function \((m,n)\mapsto 5m+8n\) from \(\mathbb{Z}^2\) to \(\mathbb{Z}\). Show that this function is
not injective;
surjective.
Solution
1. We will show that there exist pairs \((m_1,n_1)\) and \((m_2,n_2)\) in \(\mathbb{Z}^2\) such that \(5m_1+8n_1=5m_2+8n_2\) and \((m_1,n_1)\ne (m_2,n_2)\). Indeed, consider the pairs \((0,0)\) and \((8,-5)\). We have that \(5\cdot 0+8\cdot 0=5\cdot 8+8\cdot -5\) and \((0,0)\ne (8,-5)\).
2. Let \(a\) be an integer. We must show that there exists a pair \((m,n)\) in \(\mathbb{Z}^2\) such that \(5m+8n=a\). Indeed, \(5(-3a)+8(2a)=a\), so \((-3a,2a)\) has this property.
(Where did the idea for the -3 and the 2 come from in the second part of this proof? Compare with Example 3.5.1 and Example 3.5.3.)
example : ¬ Injective (fun ((m, n) : ℤ × ℤ) ↦ 5 * m + 8 * n) := by
dsimp [Injective]
push_neg
use (0, 0), (8, -5)
constructor
· numbers
· numbers
example : Surjective (fun ((m, n) : ℤ × ℤ) ↦ 5 * m + 8 * n) := by
intro a
use (-3 * a, 2 * a)
dsimp
ring
8.4.7. Example
Problem
Consider the function \((m,n)\mapsto 5m+10n\) from \(\mathbb{Z}^2\) to \(\mathbb{Z}\). Show that this function is
not injective;
not surjective.
We leave the non-injectivity proof as an exercise; it is similar to that in the previous two problems.
Solution
(Non-surjectivity) We will show that there exists an integer \(x\) such that for all pairs \((m,n)\) of integers, \(5m+10n\ne x\). Indeed, let us show that 1 has this property. Let \((m,n)\) be a pair of integers and suppose that \(5m+10n=1\). Then
contradiction.
example : ¬ Injective (fun ((m, n) : ℤ × ℤ) ↦ 5 * m + 10 * n) := by
sorry
example : ¬ Surjective (fun ((m, n) : ℤ × ℤ) ↦ 5 * m + 10 * n) := by
dsimp [Surjective]
push_neg
use 1
intro (m, n) h
dsimp at h
have :=
calc 0 ≡ 5 * (m + 2 * n) [ZMOD 5] := by extra
_ = 5 * m + 10 * n := by ring
_ = 1 := h
numbers at this
8.4.8. Example
Problem
Consider the function \(g:\mathbb{R}^2\to \mathbb{R}^2\) defined by, \(g(x,y)=(y,x)\). Show that \(g\circ g=\operatorname{Id}_\mathbb{R}\).
Solution
Let \((x,y)\) be a point in \(\mathbb{R}^2\). Then
def g : ℝ × ℝ → ℝ × ℝ
| (x, y) => (y, x)
example : g ∘ g = id := by
ext ⟨x, y⟩
dsimp [g]
8.4.9. Example
Theorem
There exists a bijection from \(\mathbb{N}^2\) to \(\mathbb{N}\).
First recall the sequence \(A_n\) from Example 6.2.4; we prove a lemma about it.
def A : ℕ → ℕ
| 0 => 0
| n + 1 => A n + n + 1
theorem A_mono {n m : ℕ} (h : n ≤ m) : A n ≤ A m := by
induction_from_starting_point m, h with k hk IH
· extra
· calc A n ≤ A k := IH
_ ≤ A k + (k + 1) := by extra
_ = A k + k + 1 := by ring
_ = A (k + 1) := by rw [A]
And a corollary, more difficult.
theorem of_A_add_mono {a1 a2 b1 b2 : ℕ} (h : A (a1 + b1) + b1 ≤ A (a2 + b2) + b2) :
a1 + b1 ≤ a2 + b2 := by
obtain h' | h' : _ ∨ a2 + b2 + 1 ≤ a1 + b1 := le_or_lt (a1 + b1) (a2 + b2)
· apply h'
rw [← not_lt] at h
have :=
calc A (a2 + b2) + b2
< A (a2 + b2) + b2 + (a2 + 1) := by extra
_ = A (a2 + b2) + (a2 + b2) + 1 := by ring
_ = A ((a2 + b2) + 1) := by rw [A]
_ = A (a2 + b2 + 1) := by ring
_ ≤ A (a1 + b1) := A_mono h'
_ ≤ A (a1 + b1) + b1 := by extra
contradiction
We use the sequence \(A_n\) to define the function \(p:\mathbb{N}^2\to \mathbb{N}\) which will be the bijection we seek: \(p(a,b)=A_{a+b}+b\).
def p : ℕ × ℕ → ℕ
| (a, b) => A (a + b) + b
Finally we prove that this function \(p\) is indeed bijective. We set up an “intertwining”
map \(i\) for \(p\), and invoke the lemma surjective_of_intertwining proved in the exercises
to Section 8.1.
def i : ℕ × ℕ → ℕ × ℕ
| (0, b) => (b + 1, 0)
| (a + 1, b) => (a, b + 1)
theorem p_comp_i (x : ℕ × ℕ) : p (i x) = p x + 1 := by
match x with
| (0, b) =>
calc p (i (0, b)) = p (b + 1, 0) := by rw [i]
_ = A ((b + 1) + 0) + 0 := by dsimp [p]
_ = A (b + 1) := by ring
_ = A b + b + 1 := by rw [A]
_ = (A (0 + b) + b) + 1 := by ring
_ = p (0, b) + 1 := by dsimp [p]
| (a + 1, b) =>
calc p (i (a + 1, b)) = p (a, b + 1) := by rw [i] ; rfl -- FIXME
_ = A (a + (b + 1)) + (b + 1) := by dsimp [p]
_ = (A ((a + 1) + b) + b) + 1 := by ring
_ = p (a + 1, b) + 1 := by rw [p]
example : Bijective p := by
constructor
· intro (a1, b1) (a2, b2) hab
dsimp [p] at hab
have H : a1 + b1 = a2 + b2
· apply le_antisymm
· apply of_A_add_mono
rw [hab]
· apply of_A_add_mono
rw [hab]
have hb : b1 = b2
· zify at hab ⊢
calc (b1:ℤ) = A (a2 + b2) + b2 - A (a1 + b1) := by addarith [hab]
_ = A (a2 + b2) + b2 - A (a2 + b2) := by rw [H]
_ = b2 := by ring
constructor
· zify at hb H ⊢
addarith [H, hb]
· apply hb
· apply surjective_of_intertwining (x0 := (0, 0)) (i := i)
· calc p (0, 0) = A (0 + 0) + 0 := by dsimp [p]
_ = A 0 := by ring
_ = 0 := by rw [A]
· intro x
apply p_comp_i
8.4.10. Exercises
Consider the function \((r,s)\mapsto (s, r-s)\) from \(\mathbb{Q}^2\) to \(\mathbb{Q}^2\). Show that this function is bijective.
example : Bijective (fun ((r, s) : ℚ × ℚ) ↦ (s, r - s)) := by rw [bijective_iff_exists_inverse] sorry
Consider the function \((x,y)\mapsto x-2y-1\) from \(\mathbb{Z}^2\) to \(\mathbb{Z}\). Show that this function is
not injective;
surjective.
example : ¬ Injective (fun ((x, y) : ℤ × ℤ) ↦ x - 2 * y - 1) := by sorry
example : Surjective (fun ((x, y) : ℤ × ℤ) ↦ x - 2 * y - 1) := by sorry
Consider the function \((x,y)\mapsto x^2+y^2\) from \(\mathbb{Q}^2\) to \(\mathbb{Q}\). Show that this function is not surjective.
example : ¬ Surjective (fun ((x, y) : ℚ × ℚ) ↦ x ^ 2 + y ^ 2) := by sorry
Consider the function \((x,y)\mapsto x^2-y^2\) from \(\mathbb{Q}^2\) to \(\mathbb{Q}\). Show that this function is surjective.
example : Surjective (fun ((x, y) : ℚ × ℚ) ↦ x ^ 2 - y ^ 2) := by sorry
Consider the function \((a,b)\mapsto a^b\) from \(\mathbb{Q}× \mathbb{N}\) to \(\mathbb{Q}\). Show that this function is surjective.
example : Surjective (fun ((a, b) : ℚ × ℕ) ↦ a ^ b) := by sorry
Consider the function \((x,y,z)\mapsto (x+y+z,x+2y+3z)\) from \(\mathbb{R}^3\) to \(\mathbb{R}^2\). Show that this function is not injective.
example : ¬ Injective (fun ((x, y, z) : ℝ × ℝ × ℝ) ↦ (x + y + z, x + 2 * y + 3 * z)) := by sorry
Consider the function \((x,y)\mapsto (x+y,x+2y, x+3y)\) from \(\mathbb{R}^2\) to \(\mathbb{R}^3\). Show that this function is injective.
example : Injective (fun ((x, y) : ℝ × ℝ) ↦ (x + y, x + 2 * y, x + 3 * y)) := by sorry
Consider the function \(h:\mathbb{R}^3\to \mathbb{R}^3\) defined by, \(h(x,y,z)=(y,z,x)\). Show that \(h\circ h\circ h=\operatorname{Id}_\mathbb{R}\).
def h : ℝ × ℝ × ℝ → ℝ × ℝ × ℝ | (x, y, z) => (y, z, x) example : h ∘ h ∘ h = id := by sorry